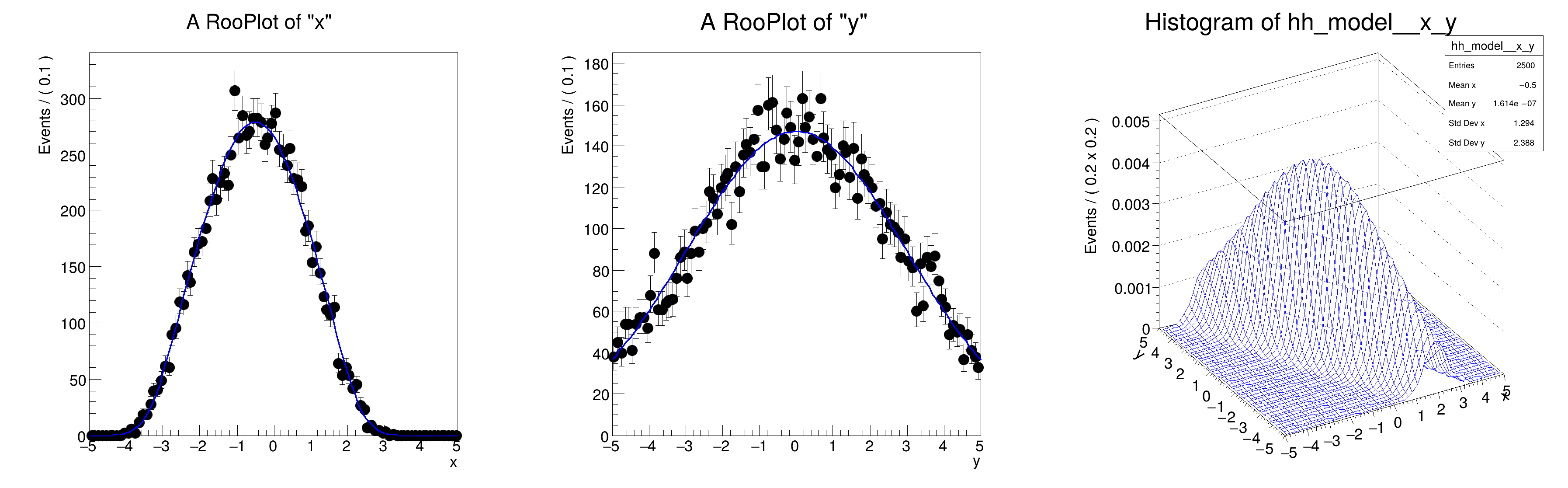
Multidimensional models: multi-dimensional pdfs with conditional pdfs in product
pdf = gauss(x,f(y),sx | y ) * gauss(y,ms,sx) with f(y) = a0 + a1*y
import ROOT
gaussx =
ROOT.RooGaussian(
"gaussx",
"Gaussian in x with shifting mean in y", x, fy, sigmax)
model =
ROOT.RooProdPdf(
"model",
"gaussx(x|y)*gaussy(y)", {gaussy}, Conditional=({gaussx}, {x}))
c =
ROOT.TCanvas(
"rf305_condcorrprod",
"rf05_condcorrprod", 1200, 400)
ROOT::Detail::TRangeCast< T, true > TRangeDynCast
TRangeDynCast is an adapter class that allows the typed iteration through a TCollection.
[#0] WARNING:InputArguments -- The parameter 'sigma' with range [-inf, inf] of the RooGaussian 'gaussx' exceeds the safe range of (0, inf). Advise to limit its range.
[#1] INFO:Plotting -- RooAbsReal::plotOn(model) plot on x integrates over variables (y)
[#1] INFO:NumericIntegration -- RooRealIntegral::init(SPECINT[gaussy_NORM[y]_X_gaussx_NORM[x]]_Int[y]) using numeric integrator RooIntegrator1D to calculate Int(y)
[#1] INFO:Plotting -- RooAbsReal::plotOn(model) plot on y integrates over variables (x)
- Date
- February 2018
- Authors
- Clemens Lange, Wouter Verkerke (C++ version)
Definition in file rf305_condcorrprod.py.