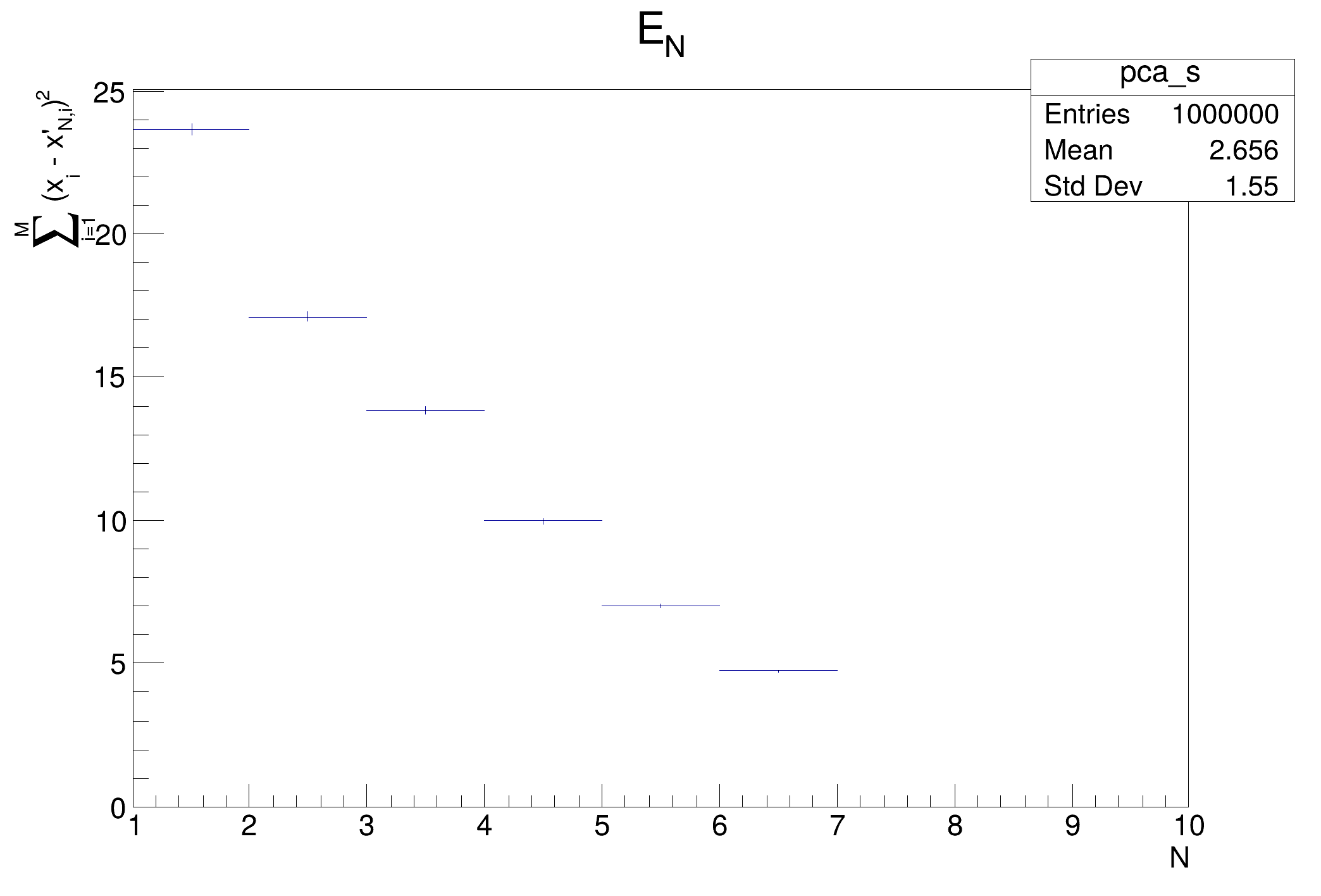
principal.C File Reference

Detailed Description

Principal Components Analysis (PCA) example

Example of using TPrincipal as a stand alone class.

We create n-dimensional data points, where c = trunc(n / 5) + 1 are correlated with the rest n - c randomly distributed variables.

 
*************************************************
*         Principal Component Analysis          *
*                                               *
*  Number of variables:             10          *
*  Number of data points:            10000      *
*  Number of dependent variables:    3          *
*                                               *
*************************************************
 Variable #  | Mean Value |   Sigma    | Eigenvalue
-------------+------------+------------+------------
           0 |      5.008 |      1.005 |     0.3851 
           1 |      7.998 |      2.861 |     0.1107 
           2 |      1.967 |      1.956 |     0.1036 
           3 |      5.016 |      1.005 |     0.1015 
           4 |      8.009 |      2.839 |     0.1008 
           5 |      2.013 |      1.973 |    0.09962 
           6 |      4.992 |      1.014 |    0.09864 
           7 |         35 |      5.156 |  6.481e-16 
           8 |      30.01 |      5.049 |  2.202e-16 
           9 |         28 |      4.649 |  5.497e-16 
 
Writing on file "pca.C" ... done

 
#include "TPrincipal.h"
 
void principal(Int_t n=10, Int_t m=10000)
{
   Int_t c = n / 5 + 1;
 
   cout << "*************************************************" << endl;
   cout << "*         Principal Component Analysis          *" << endl;
   cout << "*                                               *" << endl;
   cout << "*  Number of variables:           " << setw(4) << n
       << "          *" << endl;
   cout << "*  Number of data points:         " << setw(8) << m
       << "      *" << endl;
   cout << "*  Number of dependent variables: " << setw(4) << c
       << "          *" << endl;
   cout << "*                                               *" << endl;
   cout << "*************************************************" << endl;
 
 
   // Initilase the TPrincipal object. Use the empty string for the
   // final argument, if you don't wan't the covariance
   // matrix. Normalising the covariance matrix is a good idea if your
   // variables have different orders of magnitude.
   TPrincipal* principal = new TPrincipal(n,"ND");
 
   // Use a pseudo-random number generator
   TRandom* randomNum = new TRandom;
 
   // Make the m data-points
   // Make a variable to hold our data
   // Allocate memory for the data point
   Double_t* data = new Double_t[n];
   for (Int_t i = 0; i < m; i++) {
 
      // First we create the un-correlated, random variables, according
      // to one of three distributions
      for (Int_t j = 0; j < n - c; j++) {
         if (j % 3 == 0)      data[j] = randomNum->Gaus(5,1);
         else if (j % 3 == 1) data[j] = randomNum->Poisson(8);
         else                 data[j] = randomNum->Exp(2);
      }
 
      // Then we create the correlated variables
      for (Int_t j = 0 ; j < c; j++) {
         data[n - c + j] = 0;
         for (Int_t k = 0; k < n - c - j; k++) data[n - c + j] += data[k];
      }
 
      // Finally we're ready to add this datapoint to the PCA
      principal->AddRow(data);
   }
 
   // We delete the data after use, since TPrincipal got it by now.
   delete [] data;
 
   // Do the actual analysis
   principal->MakePrincipals();
 
   // Print out the result on
   principal->Print();
 
   // Test the PCA
   principal->Test();
 
   // Make some histograms of the original, principal, residue, etc data
   principal->MakeHistograms();
 
   // Make two functions to map between feature and pattern space
   principal->MakeCode();
 
   // Start a browser, so that we may browse the histograms generated
   // above
   TBrowser* b = new TBrowser("principalBrowser", principal);
}

Authors

Rene Brun, Christian Holm Christensen

Definition in file principal.C.