Detailed Description

Fitting multiple functions to different ranges of a 1-D histogram Example showing how to fit in a sub-range of an histogram A histogram is created and filled with the bin contents and errors defined in the table below.

Three Gaussians are fitted in sub-ranges of this histogram. A new function (a sum of 3 Gaussians) is fitted on another subrange Note that when fitting simple functions, such as Gaussians, the initial values of parameters are automatically computed by ROOT. In the more complicated case of the sum of 3 Gaussians, the initial values of parameters must be given. In this particular case, the initial values are taken from the result of the individual fits.

****************************************
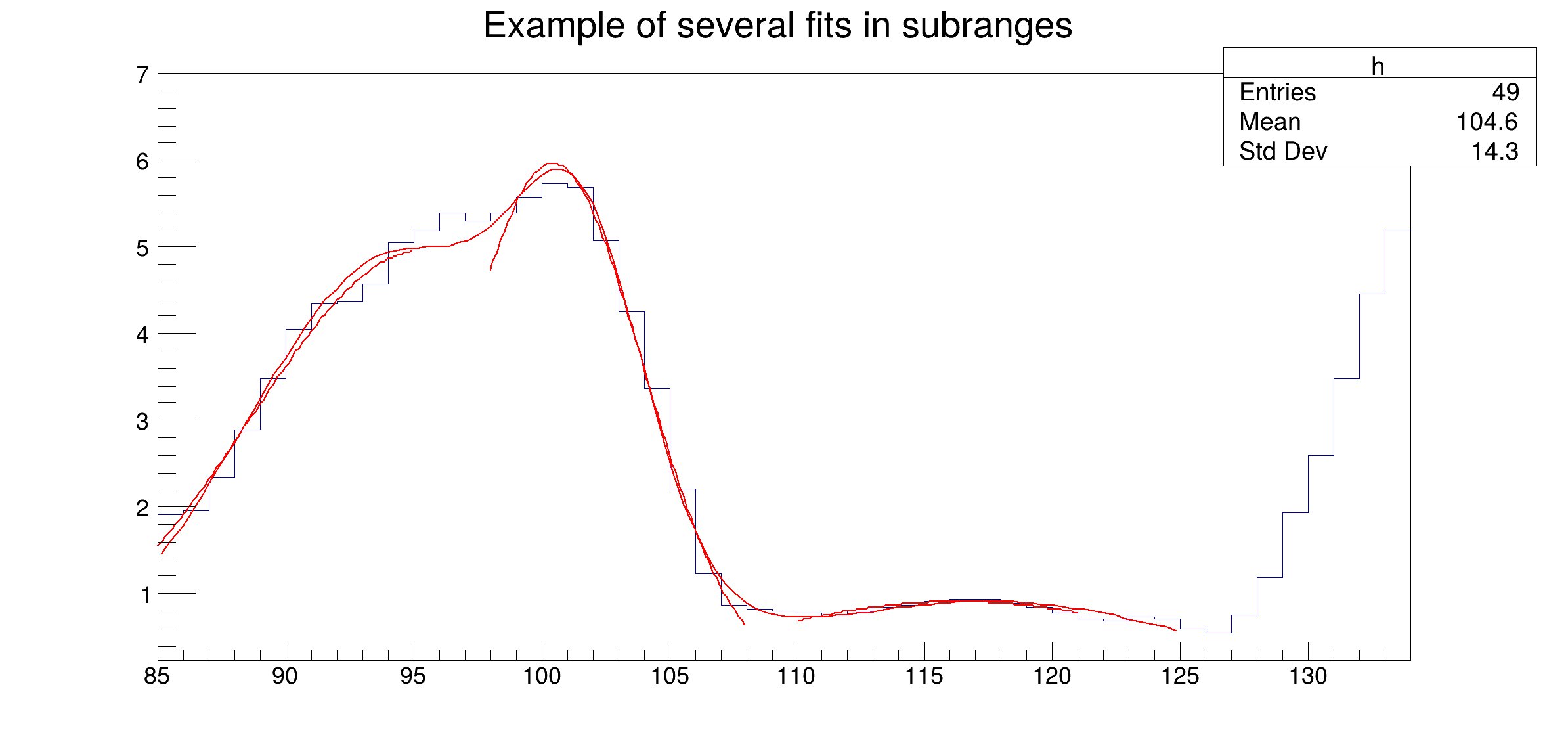
Minimizer is Minuit2 / Migrad
Chi2                      =    0.0848003
NDf                       =            7
Edm                       =  8.86911e-08
NCalls                    =          106
Constant                  =      4.96664   +/-   2.83221     
Mean                      =      95.4663   +/-   12.3905     
Sigma                     =      6.82779   +/-   7.49131        (limited)
****************************************
Minimizer is Minuit2 / Migrad
Chi2                      =    0.0771026
NDf                       =            7
Edm                       =  1.00182e-07
NCalls                    =           73
Constant                  =      5.96312   +/-   1.14355     
Mean                      =      100.467   +/-   1.53372     
Sigma                     =      3.54806   +/-   1.16899        (limited)
****************************************
Minimizer is Minuit2 / Migrad
Chi2                      =   0.00877492
NDf                       =            8
Edm                       =  4.98832e-06
NCalls                    =           87
Constant                  =     0.912053   +/-   0.435309    
Mean                      =      116.304   +/-   8.32344     
Sigma                     =      8.38103   +/-   18.5139        (limited)
****************************************
Minimizer is Minuit2 / Migrad
Chi2                      =      0.31282
NDf                       =           31
Edm                       =  3.25006e-06
NCalls                    =          495
p0                        =      4.91052   +/-   1.41324     
p1                        =      94.4492   +/-   3.71244     
p2                        =       5.9461   +/-   2.41662     
p3                        =      3.22456   +/-   3.11384     
p4                        =      101.662   +/-   1.67862     
p5                        =      2.48631   +/-   1.91151     
p6                        =     0.911626   +/-   0.368736    
p7                        =      117.581   +/-   5.06092     
p8                        =      7.59194   +/-   8.78217     
[  4.96663958  95.46632975   6.8277931    5.9631179  100.46745499
   3.54806038   0.91205321 116.30403822   8.3810307 ]

 
import ROOT
 
import numpy as np
 
n_x = 49
 
# fmt: off
x = np.array( [ 1.913521, 1.953769, 2.347435, 2.883654, 3.493567, 4.047560,
    4.337210, 4.364347, 4.563004, 5.054247, 5.194183, 5.380521, 5.303213,
    5.384578, 5.563983, 5.728500, 5.685752, 5.080029, 4.251809, 3.372246,
    2.207432, 1.227541, 0.8597788, 0.8220503, 0.8046592, 0.7684097, 0.7469761,
    0.8019787, 0.8362375, 0.8744895, 0.9143721, 0.9462768, 0.9285364,
    0.8954604, 0.8410891, 0.7853871, 0.7100883, 0.6938808, 0.7363682,
    0.7032954, 0.6029015, 0.5600163, 0.7477068, 1.188785, 1.938228, 2.602717,
    3.472962, 4.465014, 5.177035, ], dtype=np.float32,)
# fmt: on
 
# The histogram are filled with bins defined in the array x.
h = ROOT.TH1F("h", "Example of several fits in subranges", n_x, 85, 134)
h.SetMaximum(7)
 
for i, x_i in enumerate(x):
    h.SetBinContent(i + 1, x[i])
 
# Define the parameter array for the total function.
par = np.zeros(9)
 
# Three TF1 objects are created, one for each subrange.
g1 = ROOT.TF1("g1", "gaus", 85, 95)
g2 = ROOT.TF1("g2", "gaus", 98, 108)
g3 = ROOT.TF1("g3", "gaus", 110, 121)
 
# The total is the sum of the three, each has three parameters.
total = ROOT.TF1("total", "gaus(0)+gaus(3)+gaus(6)", 85, 125)
total.SetLineColor(2)
 
# The canvas that the histograms and fit functions are drawn on.
c = ROOT.TCanvas("multifit", "multifit", 800, 400)
 
# Fit each function and add it to the list of functions. By default, TH1::Fit()
# fits the function on the defined histogram range. You can specify the "R"
# option in the second parameter of TH1::Fit() to restrict the fit to the range
# specified in the TF1 constructor. Alternatively, you can also specify the
# range in the call to TH1::Fit(), which we demonstrate here with the 3rd
# Gaussian. The "+" option needs to be added to the later fits to not replace
# existing fitted functions in the histogram.
h.Fit(g1, "R")
h.Fit(g2, "R+")
h.Fit(g3, "+", "", 110, 121);
 
# Get the parameters from the fit.
g1.GetParameters(par[:3])
g2.GetParameters(par[3:6])
g3.GetParameters(par[6:])
 
print(par)
 
# Use the parameters on the sum.
total.SetParameters(par)
 
h.Draw()
h.Fit(total, "R+")
 
# Save the plot for later inspection.
c.SaveAs("multifit.png")

Authors: Jonas Rembser, Rene Brun (C++ version)

Definition in file multifit.py.