

Example of random number generation by sampling a multi-dim distribution using the DistSampler class.
NOTE: This tutorial must be run with ACLIC

#include <cmath>
{}
int k = 0;
for (
int i = 0; i<dim; ++i) {
X[i] =
x[i] -
p[k]; k++; }
for (int i = 0; i<dim; ++i) {
k++;
}
for (int i = 0; i<dim; ++i) {
for (
int j = i+1;
j<dim; ++
j) {
k++;
}
}
}
Fatal(
"GausND",
"Determinant is <= 0 det = %f",
det);
return 0;
}
std::cout <<
"det " <<
det << std::endl;
std::cout <<
"norm " <<
norm << std::endl;
std::cout <<
"fval " <<
fval << std::endl;
}
}
};
double xmin[] = {-10,-10,-10, -10};
double xmax[] = { 10, 10, 10, 10};
double par0[] = { 1., -1., 2, 0,
1, 2, 1, 3,
0.5,0.,0.,0.,0.,0.8 };
double x0[] = {0,0,0,0};
if (
debug)
f->EvalPar(x0,
nullptr);
for (
int i = 0; i <
NPAR; ++i ) {
if (i <
DIM)
f->SetParName(i,
name.Format(
"mu_%d",i+1) );
else if (i < 2*
DIM)
f->SetParName(i,
name.Format(
"sig_%d",i-
DIM+1) );
else if (i < 2*
DIM)
f->SetParName(i,
name.Format(
"sig_%d",i-2*
DIM+1) );
}
Info(
"multidimSampling",
"Default sampler %s is not available try with Foam ",
}
sampler = Factory::CreateDistSampler();
Error(
"multidimSampling",
"Foam sampler is not available - exit ");
return;
}
Error(
"Sampler::Init",
"Error initializing unuran sampler");
return;
}
for (
int i = 0; i <
N; ++i) {
}
TFile * file =
new TFile(
"multiDimSampling.root",
"RECREATE");
t1->Branch(
"x",
x,
"x[4]/D");
for (
int i = 0; i <
N; ++i) {
for (
int j = 0;
j <
DIM; ++
j) {
}
}
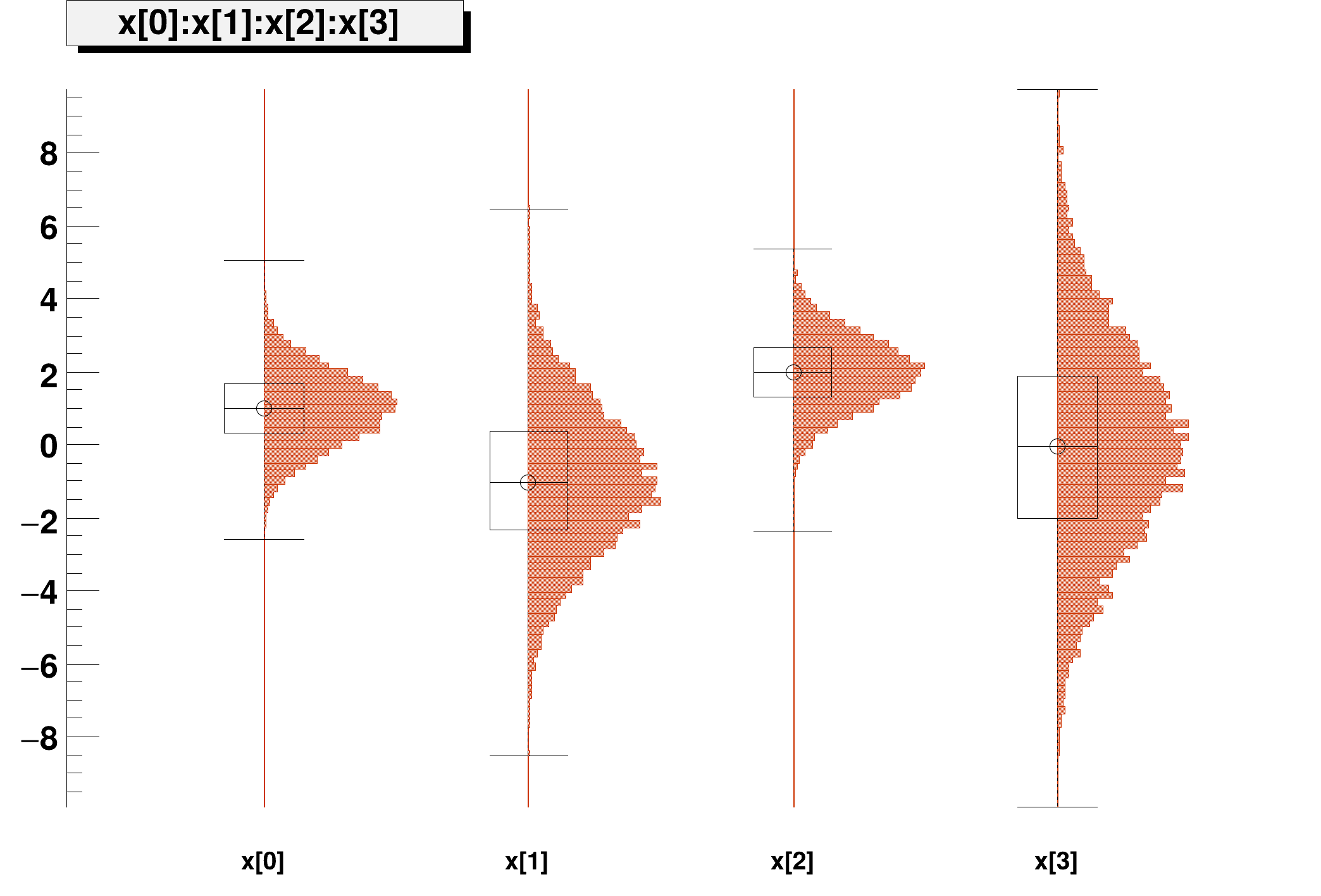
t1->Draw(
"x[0]:x[1]:x[2]:x[3]",
"",
"candle");
}
ROOT::Detail::TRangeCast< T, true > TRangeDynCast
TRangeDynCast is an adapter class that allows the typed iteration through a TCollection.
void Info(const char *location, const char *msgfmt,...)
Use this function for informational messages.
void Error(const char *location, const char *msgfmt,...)
Use this function in case an error occurred.
void Fatal(const char *location, const char *msgfmt,...)
Use this function in case of a fatal error. It will abort the program.
winID h TVirtualViewer3D TVirtualGLPainter p
TRObject operator()(const T1 &t1) const
static void SetDefaultSampler(const char *type)
static const std::string & DefaultSampler()
Interface class for generic sampling of a distribution, i.e.
A ROOT file is an on-disk file, usually with extension .root, that stores objects in a file-system-li...
void Close(Option_t *option="") override
Close a file.
A TTree represents a columnar dataset.
- Author
- Lorenzo Moneta
Definition in file multidimSampling.C.



