double32.C File Reference

Detailed Description

Tutorial illustrating use and precision of the Double32_t data type You should run this tutorial with ACLIC: a dictionary will be automatically created.

root > .x double32.C+

The following cases are supported for streaming a Double32_t type depending on the range declaration in the comment field of the data member:

Case	Declaration
A	Double32_t fNormal;
B	Double32_t fTemperature; //[0,100]
C	Double32_t fCharge; //[-1,1,2]
D	Double32_t fVertex[3]; //[-30,30,10]
E	Double32_t fChi2; //[0,0,6]
F	Int_t fNsp; Double32_t* fPointValue; //[fNsp][0,3]

• Case A fNormal is converted from a Double_t to a Float_t
• Case B fTemperature is converted to a 32 bit unsigned integer
• Case C fCharge is converted to a 2 bits unsigned integer
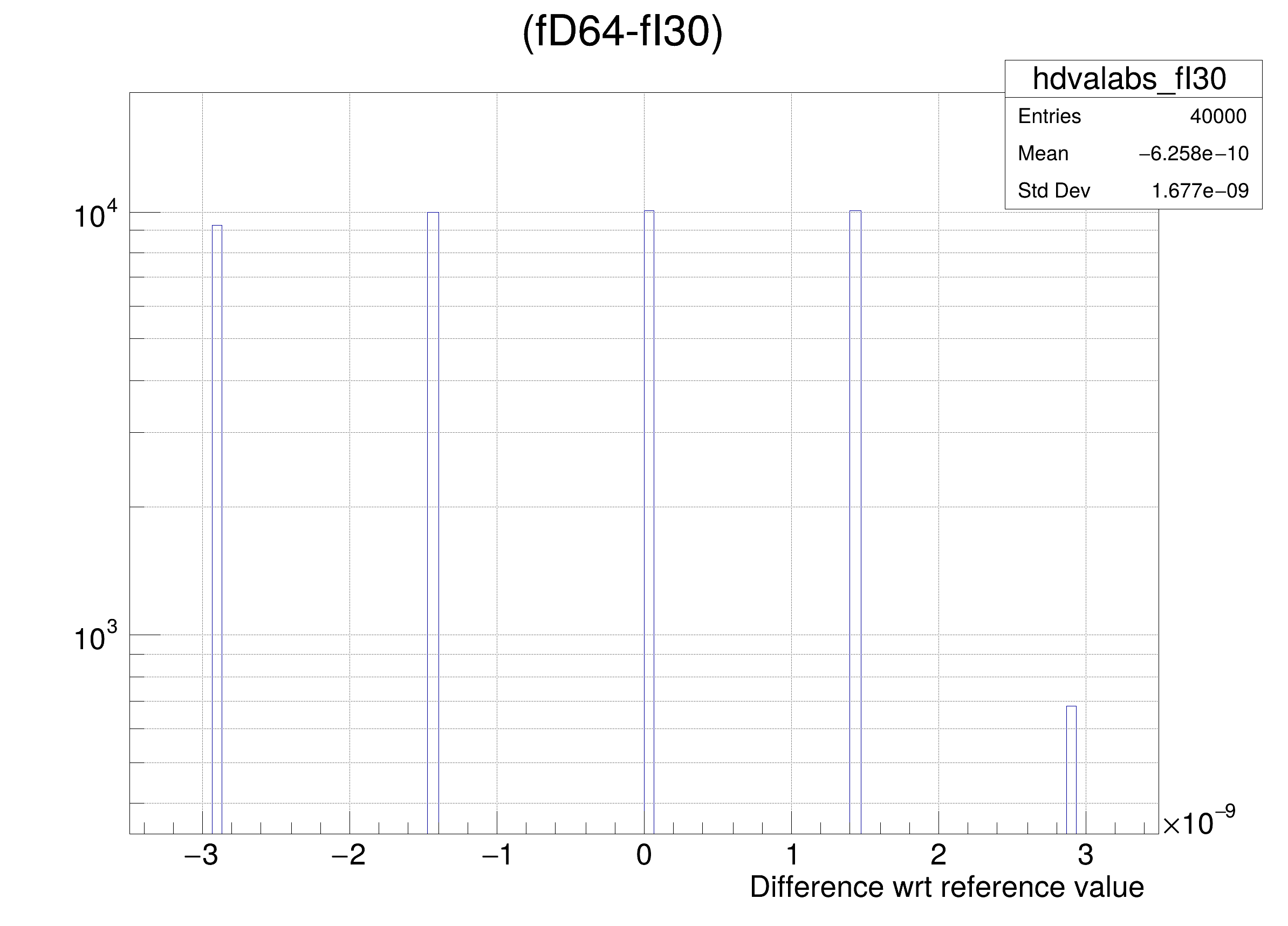
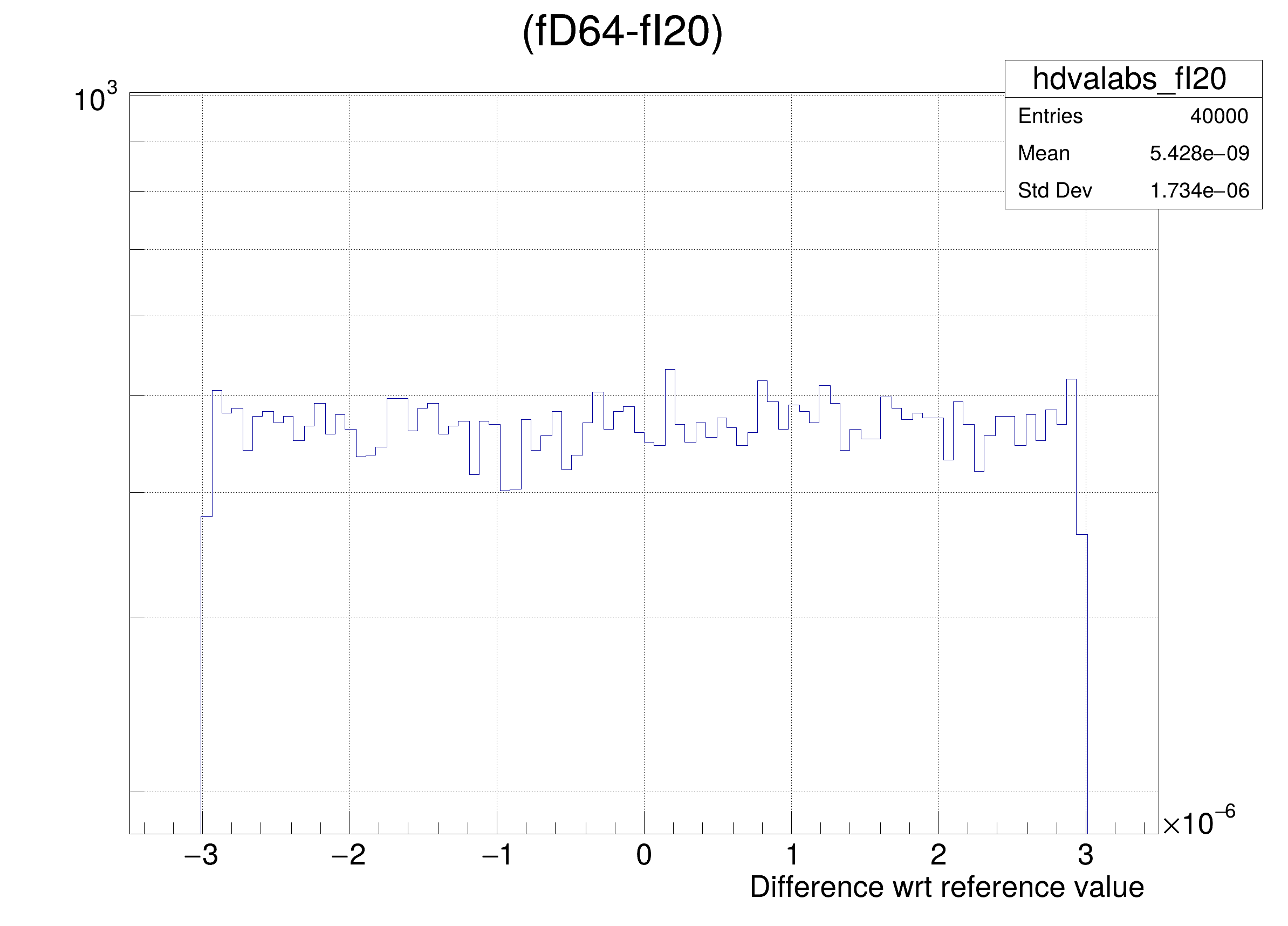
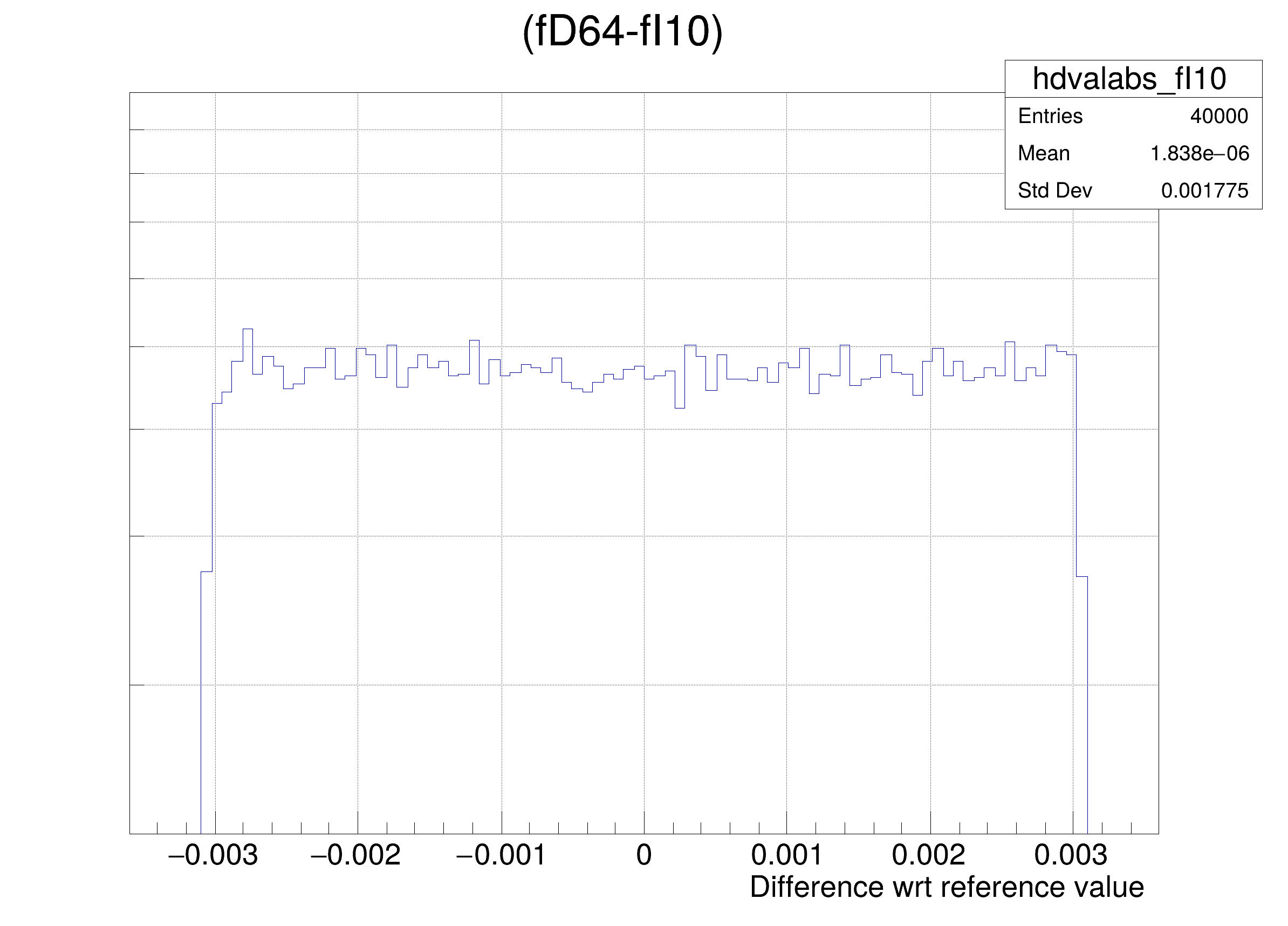
• Case D the array elements of fVertex are converted to an unsigned 10 bits integer
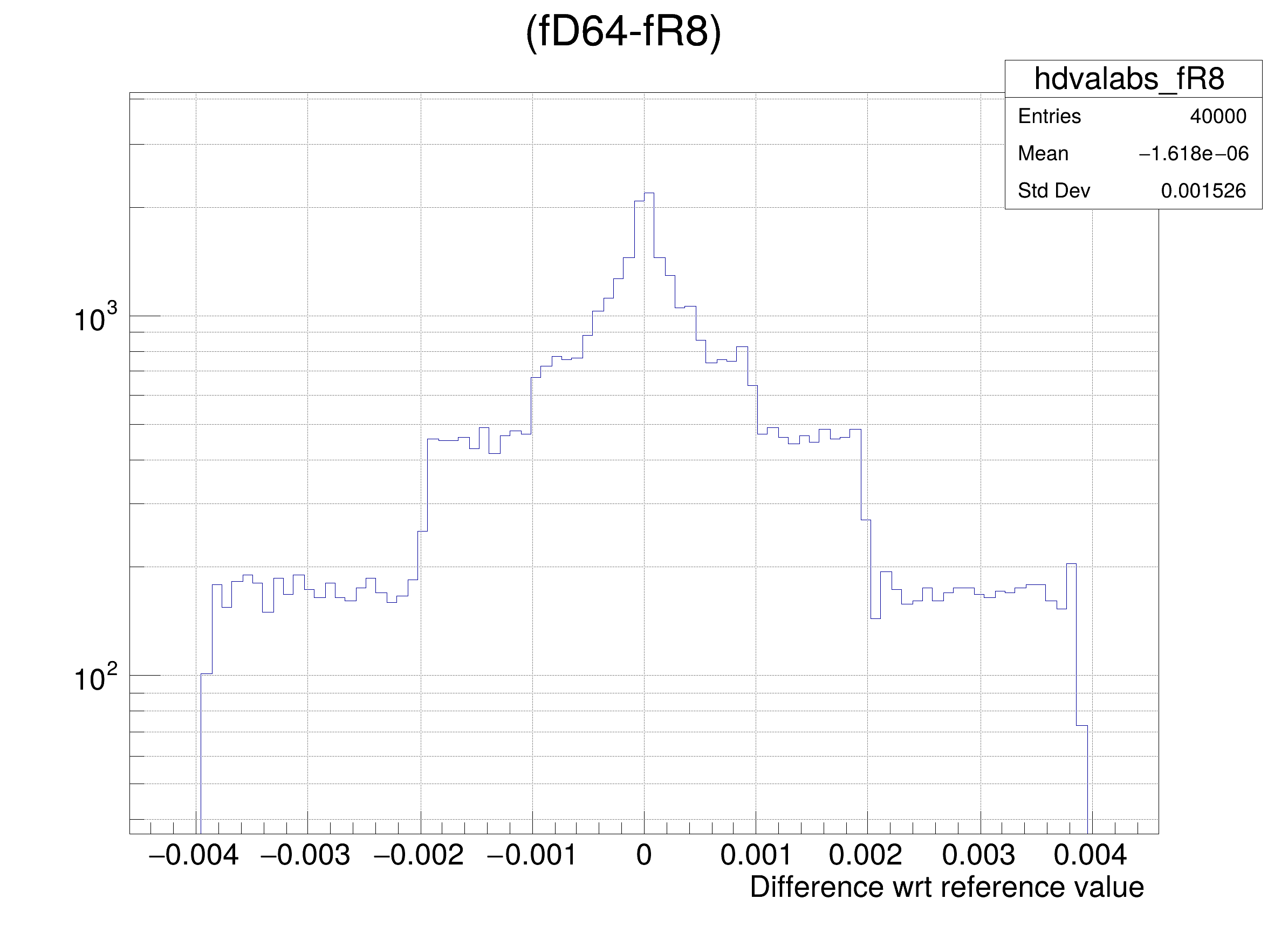
• Case E fChi2 is converted to a Float_t with truncated precision at 6 bits
• Case F the fNsp elements of array fPointvalue are converted to an unsigned 32 bit integer. Note that the range specifier must follow the dimension specifier.

Case B has more precision than case A: 9 to 10 significative digits and 6 to 7 digits respectively. The range specifier has the general format: [xmin,xmax] or [xmin,xmax,nbits]. Examples

• [0,1]
• [-10,100];
• [-pi,pi], [-pi/2,pi/4],[-2pi,2*pi]
• [-10,100,16]
• [0,0,8] Note that:
• If nbits is not specified, or nbits <2 or nbits>32 it is set to 32
• If (xmin==0 and xmax==0 and nbits <=14) the double word will be converted to a float and its mantissa truncated to nbits significative bits.

IMPORTANT NOTE

Lets assume an original variable double x. When using the format [0,0,8] (i.e. range not specified) you get the best relative precision when storing and reading back the truncated x, say xt. The variance of (x-xt)/x will be better than when specifying a range for the same number of bits. However the precision relative to the range (x-xt)/(xmax-xmin) will be worse, and vice-versa. The format [0,0,8] is also interesting when the range of x is infinite or unknown.

 
#include "ROOT/TSeq.hxx"
#include "TCanvas.h"
#include "TFile.h"
#include "TGraph.h"
#include "TH1.h"
#include "TLegend.h"
#include "TMath.h"
#include "TRandom3.h"
#include "TTree.h"
 
class DemoDouble32 {
private:
   Double_t fD64;   // reference member with full double precision
   Double32_t fF32; // saved as a 32 bit Float_t
   Double32_t fI32; //[-pi,pi]    saved as a 32 bit unsigned int
   Double32_t fI30; //[-pi,pi,30] saved as a 30 bit unsigned int
   Double32_t fI28; //[-pi,pi,28] saved as a 28 bit unsigned int
   Double32_t fI26; //[-pi,pi,26] saved as a 26 bit unsigned int
   Double32_t fI24; //[-pi,pi,24] saved as a 24 bit unsigned int
   Double32_t fI22; //[-pi,pi,22] saved as a 22 bit unsigned int
   Double32_t fI20; //[-pi,pi,20] saved as a 20 bit unsigned int
   Double32_t fI18; //[-pi,pi,18] saved as a 18 bit unsigned int
   Double32_t fI16; //[-pi,pi,16] saved as a 16 bit unsigned int
   Double32_t fI14; //[-pi,pi,14] saved as a 14 bit unsigned int
   Double32_t fI12; //[-pi,pi,12] saved as a 12 bit unsigned int
   Double32_t fI10; //[-pi,pi,10] saved as a 10 bit unsigned int
   Double32_t fI8;  //[-pi,pi, 8] saved as a  8 bit unsigned int
   Double32_t fI6;  //[-pi,pi, 6] saved as a  6 bit unsigned int
   Double32_t fI4;  //[-pi,pi, 4] saved as a  4 bit unsigned int
   Double32_t fI2;  //[-pi,pi, 2] saved as a  2 bit unsigned int
   Double32_t fR14; //[0,  0, 14] saved as a 32 bit float with a 14 bits mantissa
   Double32_t fR12; //[0,  0, 12] saved as a 32 bit float with a 12 bits mantissa
   Double32_t fR10; //[0,  0, 10] saved as a 32 bit float with a 10 bits mantissa
   Double32_t fR8;  //[0,  0,  8] saved as a 32 bit float with a  8 bits mantissa
   Double32_t fR6;  //[0,  0,  6] saved as a 32 bit float with a  6 bits mantissa
   Double32_t fR4;  //[0,  0,  4] saved as a 32 bit float with a  4 bits mantissa
   Double32_t fR2;  //[0,  0,  2] saved as a 32 bit float with a  2 bits mantissa
 
public:
   DemoDouble32() = default;
   void Set(Double_t ref)
   {
      fD64 = fF32 = fI32 = fI30 = fI28 = fI26 = fI24 = fI22 = fI20 = fI18 = fI16 = fI14 = fI12 = fI10 = fI8 = fI6 =
         fI4 = fI2 = fR14 = fR12 = fR10 = fR8 = fR6 = fR4 = fR2 = ref;
   }
};
 
void double32()
{
   const auto nEntries = 40000;
   const auto xmax = TMath::Pi();
   const auto xmin = -xmax;
 
   // create a Tree with nEntries objects DemoDouble32
   TFile::Open("DemoDouble32.root", "recreate");
   DemoDouble32 demoInstance;
   TRandom3 r;
   for (auto i : ROOT::TSeqI(nEntries)) {
      demoInstance.Set(r.Uniform(xmin, xmax));
   }
 
   // Now we can proceed with the analysis of the sizes on disk of all branches
 
   // Create the frame histogram and the graphs
   auto branches = demoInstanceBranch->GetListOfBranches();
   const auto nb = branches->GetEntries();
   auto br = static_cast<TBranch *>(branches->At(0));
   const Long64_t zip64 = br->GetZipBytes();
 
   auto h = new TH1F("h", "Double32_t compression and precision", nb, 0, nb);
   h->SetMaximum(18);
   h->SetStats(false);
 
   auto gcx = new TGraph();
   gcx->SetName("gcx");
   gcx->SetMarkerStyle(kFullSquare);
   gcx->SetMarkerColor(kBlue);
 
   auto gdrange = new TGraph();
   gdrange->SetName("gdrange");
   gdrange->SetMarkerStyle(kFullCircle);
   gdrange->SetMarkerColor(kRed);
 
   auto gdval = new TGraph();
   gdval->SetName("gdval");
   gdval->SetMarkerStyle(kFullTriangleUp);
   gdval->SetMarkerColor(kBlack);
 
   // loop on branches to get the precision and compression factors
   for (auto i : ROOT::TSeqI(nb)) {
      auto br = static_cast<TBranch *>(branches->At(i));
      const auto brName = br->GetName();
 
      h->GetXaxis()->SetBinLabel(i + 1, brName);
      const auto cx = double(zip64) / br->GetZipBytes();
      gcx->SetPoint(i, i + 0.5, cx);
      if (i == 0 ) continue;
 
      const auto drange = TMath::Max(0., -TMath::Log10(rmsDrange));
      gdrange->SetPoint(i-1, i + 0.5, drange);
 
      const auto dval = TMath::Max(0., -TMath::Log10(rmsDVal));
      gdval->SetPoint(i-1, i + 0.5, dval);
 
      auto hdval = gDirectory->Get<TH1F>(Form("hdvalabs_%s", brName));
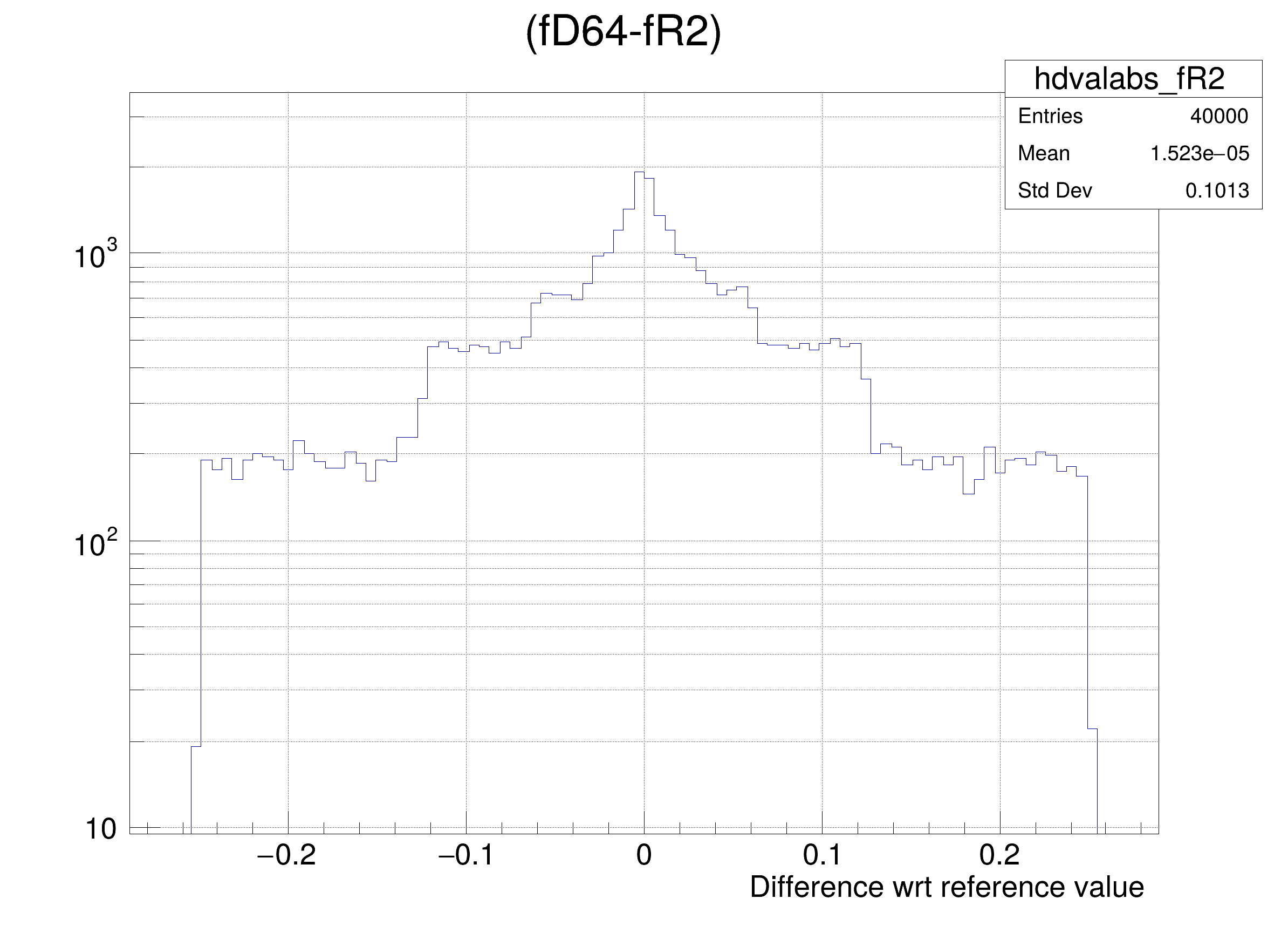
      hdval->GetXaxis()->SetTitle("Difference wrt reference value");
      auto c = new TCanvas(brName, brName, 800, 600);
      c->SetGrid();
      c->SetLogy();
      hdval->DrawClone();
   }
   
   auto c1 = new TCanvas("c1", "c1", 800, 600);
   c1->SetGrid();
 
   h->Draw();
   h->GetXaxis()->LabelsOption("v");
   gcx->Draw("lp");
   gdrange->Draw("lp");
   gdval->Draw("lp");
 
   // Finally build a legend
   auto legend = new TLegend(0.3, 0.6, 0.9, 0.9);
   legend->SetHeader(Form("%d entries within the [-#pi, #pi] range", nEntries));
   legend->AddEntry(gcx, "Compression factor", "lp");
   legend->AddEntry(gdrange, "Log of precision wrt range: p = -Log_{10}( RMS( #frac{Ref - x}{range} ) ) ", "lp");
   legend->AddEntry(gdval, "Log of precision wrt value: p = -Log_{10}( RMS( #frac{Ref - x}{Ref} ) ) ", "lp");
   legend->Draw();
}

Author

Rene Brun

Definition in file double32.C.