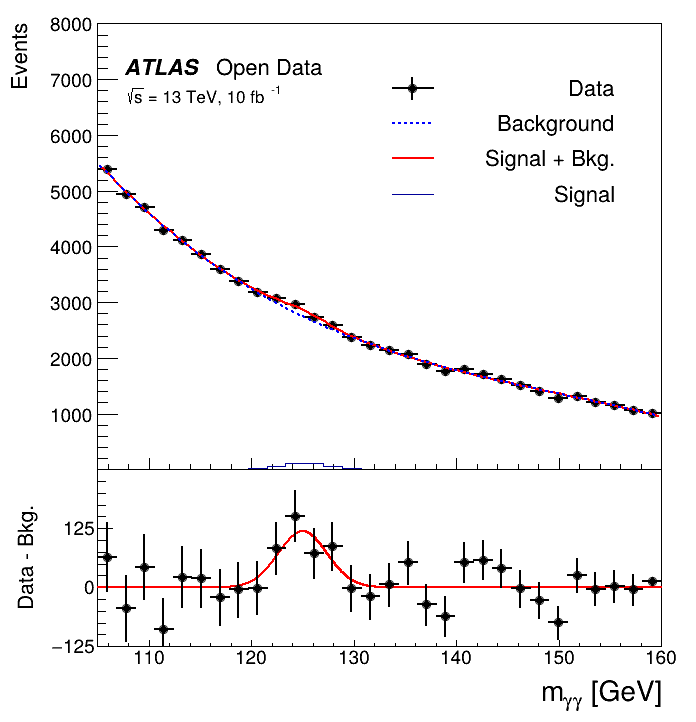
This tutorial is the Higgs to two photons analysis from the ATLAS Open Data release in 2020 (http://opendata.atlas.cern/release/2020/documentation/). The data was taken with the ATLAS detector during 2016 at a center-of-mass energy of 13 TeV. Although the Higgs to two photons decay is very rare, the contribution of the Higgs can be seen as a narrow peak around 125 GeV because of the excellent reconstruction and identification efficiency of photons at the ATLAS experiment.
The analysis is translated to a RDataFrame workflow processing 1.7 GB of simulated events and data.
import ROOT
import os
path = "root://eospublic.cern.ch//eos/opendata/atlas/OutreachDatasets/2020-01-22"
df = {}
for p in ["ggH", "VBF"]:
df[p] = df[p].Define("weight",
"scaleFactor_PHOTON * scaleFactor_PhotonTRIGGER * scaleFactor_PILEUP * mcWeight");
df["data"] = df["data"].Define("weight", "1.0")
for p in processes:
df[p] = df[p].Filter("trigP")
df[p] = df[p].Define("goodphotons", "photon_isTightID && (photon_pt > 25000) && (abs(photon_eta) < 2.37) && ((abs(photon_eta) < 1.37) || (abs(photon_eta) > 1.52))")\
.Filter("Sum(goodphotons) == 2")
df[p] = df[p].Filter("Sum(photon_ptcone30[goodphotons] / photon_pt[goodphotons] < 0.065) == 2")\
.Filter("Sum(photon_etcone20[goodphotons] / photon_pt[goodphotons] < 0.065) == 2")
"""
using namespace ROOT;
float ComputeInvariantMass(RVecF pt, RVecF eta, RVecF phi, RVecF e) {
ROOT::Math::PtEtaPhiEVector p1(pt[0], eta[0], phi[0], e[0]);
ROOT::Math::PtEtaPhiEVector p2(pt[1], eta[1], phi[1], e[1]);
return (p1 + p2).mass() / 1000.0;
}
""")
hists = {}
for p in processes:
df[p] = df[p].Define("m_yy", "ComputeInvariantMass(photon_pt[goodphotons], photon_eta[goodphotons], photon_phi[goodphotons], photon_E[goodphotons])")
df[p] = df[p].Filter("photon_pt[goodphotons][0] / 1000.0 / m_yy > 0.35")\
.Filter("photon_pt[goodphotons][1] / 1000.0 / m_yy > 0.25")\
.Filter("m_yy > 105 && m_yy < 160")
hists[p] = df[p].Histo1D(
ROOT.RDF.TH1DModel(p,
"Diphoton invariant mass; m_{#gamma#gamma} [GeV];Events", 30, 105, 160),
"m_yy", "weight")
ggh = hists["ggH"].GetValue()
vbf = hists["VBF"].GetValue()
data = hists["data"].GetValue()
upper_pad =
ROOT.TPad(
"upper_pad",
"", 0, 0.35, 1, 1)
lower_pad =
ROOT.TPad(
"lower_pad",
"", 0, 0, 1, 0.35)
for p in [upper_pad, lower_pad]:
fit =
ROOT.TF1(
"fit",
"([0]+[1]*x+[2]*x^2+[3]*x^3)+[4]*exp(-0.5*((x-[5])/[6])^2)", 105, 160)
bkg =
ROOT.TF1(
"bkg",
"([0]+[1]*x+[2]*x^2+[3]*x^3)", 105, 160)
lumi = 10064.0
vbf.Scale(lumi * 0.008518764 / 3441426.13711)
ratiobkg =
ROOT.TH1I(
"zero",
"", 100, 105, 160)
ratiosig =
ROOT.TH1F(
"ratiosig",
"ratiosig", 5500, 105, 160)
print("Saved figure to df104_HiggsToTwoPhotons.png")
ROOT::Detail::TRangeCast< T, true > TRangeDynCast
TRangeDynCast is an adapter class that allows the typed iteration through a TCollection.
Option_t Option_t TPoint TPoint const char GetTextMagnitude GetFillStyle GetLineColor GetLineWidth GetMarkerStyle GetTextAlign GetTextColor GetTextSize void char Point_t Rectangle_t WindowAttributes_t Float_t Float_t Float_t Int_t Int_t UInt_t UInt_t Rectangle_t Int_t Int_t Window_t TString Int_t GCValues_t GetPrimarySelectionOwner GetDisplay GetScreen GetColormap GetNativeEvent const char const char dpyName wid window const char font_name cursor keysym reg const char only_if_exist regb h Point_t winding char text const char depth char const char Int_t count const char ColorStruct_t color const char Pixmap_t Pixmap_t PictureAttributes_t attr const char char ret_data h unsigned char height h Atom_t Int_t ULong_t ULong_t unsigned char prop_list Atom_t Atom_t Atom_t Time_t format
ROOT's RDataFrame offers a modern, high-level interface for analysis of data stored in TTree ,...
A struct which stores some basic parameters of a TH1D.
****************************************
Minimizer is Minuit2 / Migrad
Chi2 = 19.9699
NDf = 26
Edm = 2.71045e-09
NCalls = 161
p0 = 94325 +/- 72.0526
p1 = -1777.22 +/- 0.778156
p2 = 11.5606 +/- 0.00536059
p3 = -0.0256281 +/- 2.66824e-05
p4 = 119.1 (fixed)
p5 = 125 (fixed)
p6 = 2.39 (fixed)
Saved figure to df104_HiggsToTwoPhotons.png