Adding control points

You can add control points to a curve without changing its shape. This process is called refinement or knot insertion. Knot insertion is a way of adding more flexibility to a curve and limiting the effect on a curve when a control point is moved.

The total number of knots is equal to the order plus the number of control points. Each time you add a knot, another control point is added to the curve. The placement of the new point depends on the value of the new knot. Curve refinement moves the other control points near the new control point to preserve the shape of the curve. As you add more knots, the control points get closer and closer to the actual curve. When a control point is moved, its effect varies according to the order of the curve. If the order is high, moving a single control point affects more of the curve than if the order is low. The higher the order, the longer it takes to render the curve.

The following functions let you insert and refine knots.

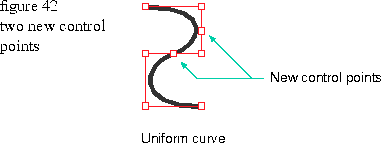
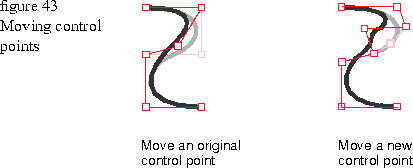
 In Figure 42 below, the original knot vector was [0 0 0 0 1 2 3 3 3 3]. To add more flexibility, two control points are added at 1.5 and 2.5 to make the knot vector [0 0 0 0 1 1.5 2 2.5 3 3 3 3].


Figure 43 shows how portions of the curve change when you move one of the original control points and then move one of the added control points.


If you insert multiple knots with the same values, you introduce the discontinuities described before, but the kink or break do not appear until you move the control points.

NOTE Some textbooks suggest that you place two or three control points at the same location to create discontinuities. This approach is not recommended because it forces a portion of the curve on either side of the multiple control point to become a straight line.

[Contents] [Previous] [Next]
Click the icon to mail questions or corrections about this material to Taligent personnel.
Copyright©1995 Taligent,Inc. All rights reserved.

Generated with WebMaker