






Common knot vectors
A knot vector is a sequence of parameter values for determining the continuity along a curve's length. Common knot vectors are the pinned uniform and the piecewise Bézier. Pinned uniform is the most common knot vector.
Pinned knot vector
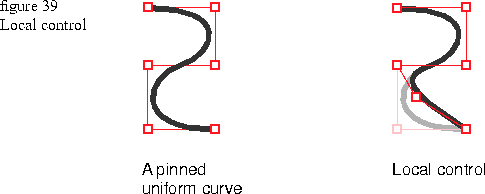
In a pinned knot vector, the curve passes through the starting control point and the ending control point (pinned at the endpoints) while the points in between pass near the control points but do not necessarily go through them. If the number of control points equals the order, moving any control point changes the shape of the entire curve. If the number of control points exceeds the order, moving a particular point affects only the curve near the point, called local control as shown in Figure 39
.
NOTE  A pinned uniform curve with the number of control points equal to the order is by definition a Bézier curve.
A pinned uniform curve with the number of control points equal to the order is by definition a Bézier curve.
Piecewise Bézier
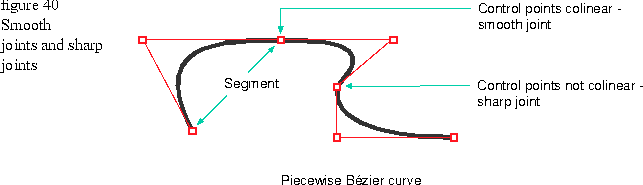
The piecewise Bézier knot vector is usually used when many simple primitives such as arcs, lines, or simple curve segments are strung together into a single large curve. If k represents the order, the curve passes through each k'th control point on the curve and passes near all of the other control points, which breaks the curve into segments of k points each. Moving a control point within a segment affects only that segment, and moving a point where two segments join affects both segments. If the joint and the control points on either side of the joint are in a straight line, the two segments form a smooth continuous curve. Otherwise, a sharp kink or discontinuity occurs as shown in Figure 40
.
In a piecewise Bézier knot vector, the knots follow a pattern based on the order of the curve and the number of control points. A piecewise Bézier curve must have nk+1 control points, where n is the number of segments and k is the order. That is, the number of control points is one more than an even multiple of the order.
The knot vector pattern is as follows: The first k knots have the same knot value, the next k-1 knots have the same knot value, and the last k knots have the same knot value. A quadratic (order 3) piecewise Bézier knot vector with seven control points has ten knots (7 plus 3) that look like this: [0 0 0 1 1 2 2 3 3 3].
The following functions let you set and reset the type of knot vector:
- TCurve::SetKnotScheme( kPinned ) function resets a knot vector to pinned uniform.
- TCurve::SetKnotScheme( kBezier ) resets the knot vector to piecewise Bézier.
[Contents]
[Previous]
[Next]
 Click the icon to mail questions or corrections about this material to Taligent personnel.
Click the icon to mail questions or corrections about this material to Taligent personnel.
Copyright©1995 Taligent,Inc. All rights reserved.
Generated with WebMaker

 A pinned uniform curve with the number of control points equal to the order is by definition a Bézier curve.
A pinned uniform curve with the number of control points equal to the order is by definition a Bézier curve.