library: libHist
#include "TGraph2D.h" |
TGraph2D
class description - source file - inheritance tree (.pdf)
protected:
void Build(Int_t n)
public:
TGraph2D()
TGraph2D(Int_t n)
TGraph2D(Int_t n, Int_t* x, Int_t* y, Int_t* z)
TGraph2D(Int_t n, Float_t* x, Float_t* y, Float_t* z)
TGraph2D(Int_t n, Double_t* x, Double_t* y, Double_t* z)
TGraph2D(TH2* h2)
TGraph2D(const char* name, const char* title, Int_t n, Double_t* x, Double_t* y, Double_t* z)
TGraph2D(const char* filename, const char* format = "%lg %lg %lg", Option_t* option)
TGraph2D(const TGraph2D&)
TGraph2D operator=(const TGraph2D&)
virtual ~TGraph2D()
static TClass* Class()
virtual Int_t DistancetoPrimitive(Int_t px, Int_t py)
virtual void Draw(Option_t* option)
virtual void ExecuteEvent(Int_t event, Int_t px, Int_t py)
virtual TObject* FindObject(const char* name) const
virtual TObject* FindObject(const TObject* obj) const
virtual Int_t Fit(const char* formula, Option_t* option, Option_t* goption)
virtual Int_t Fit(TF2* f2, Option_t* option, Option_t* goption)
TList* GetContourList(Double_t contour)
TDirectory* GetDirectory() const
virtual Double_t GetErrorX(Int_t bin) const
virtual Double_t GetErrorY(Int_t bin) const
virtual Double_t GetErrorZ(Int_t bin) const
TH2D* GetHistogram(Option_t* option)
TList* GetListOfFunctions() const
Double_t GetMargin() const
Int_t GetN() const
Int_t GetNpx() const
Int_t GetNpy() const
Double_t* GetX() const
TAxis* GetXaxis() const
Double_t GetXmax() const
Double_t GetXmin() const
Double_t* GetY() const
TAxis* GetYaxis() const
Double_t GetYmax() const
Double_t GetYmin() const
Double_t* GetZ() const
TAxis* GetZaxis() const
Double_t GetZmax() const
Double_t GetZmin() const
Double_t Interpolate(Double_t x, Double_t y)
virtual TClass* IsA() const
virtual void Paint(Option_t* option)
TH1* Project(Option_t* option = "x") const
Int_t RemovePoint(Int_t ipoint)
virtual void SavePrimitive(ofstream& out, Option_t* option)
virtual void SetDirectory(TDirectory* dir)
void SetMargin(Double_t m = 0.1)
void SetMarginBinsContent(Double_t z = 0.)
void SetMaximum(Double_t maximum = -1111)
void SetMaxIter(Int_t n = 100000)
void SetMinimum(Double_t minimum = -1111)
virtual void SetName(const char* name)
void SetNpx(Int_t npx = 40)
void SetNpy(Int_t npx = 40)
void SetPoint(Int_t point, Double_t x, Double_t y, Double_t z)
virtual void SetTitle(const char* title)
virtual void ShowMembers(TMemberInspector& insp, char* parent)
virtual void Streamer(TBuffer& b)
void StreamerNVirtual(TBuffer& b)
protected:
Int_t fNpoints Number of points in the data set
Int_t fNpx Number of bins along X in fHistogram
Int_t fNpy Number of bins along Y in fHistogram
Int_t fMaxIter Maximum number of iterations to find Delaunay t>
Int_t fSize !Real size of fX, fY and fZ
Double_t* fX [fNpoints]
Double_t* fY [fNpoints] Data set to be plotted
Double_t* fZ [fNpoints]
Double_t fMinimum Minimum value for plotting along z
Double_t fMaximum Maximum value for plotting along z
Double_t fMargin Extra space (in %) around interpolated area for fHistogram
Double_t fZout fHistogram bin height for points lying outside the interpolated area
TList* fFunctions Pointer to list of functions (fits and user)
TH2D* fHistogram !2D histogram of z values linearly interpolated
TDirectory* fDirectory !Pointer to directory holding this 2D graph
TVirtualHistPainter* fPainter !pointer to histogram painter
public:
static const enum TGraph2D:: kFitInit
A Graph2D is a graphics object made of three arrays X, Y and Z with the same
number of points each.
This class has different constructors:
1) With an array's dimension and three arrays x, y, and z:
TGraph2D *g = new TGraph2D(n, x, y, z);
x, y, z arrays can be doubles, floats, or ints.
2) With an array's dimension only:
TGraph2D *g = new TGraph2D(n);
The internal arrays are then filled with SetPoint. The following line
fills the the internal arrays at the position "i" with the values x,y,z.
g->SetPoint(i, x, y, z);
3) Without parameters:
TGraph2D *g = new TGraph2D();
again SetPoint must be used to fill the internal arrays.
4) From a file:
TGraph2D *g = new TGraph2D("graph.dat");
Arrays are read from the ASCII file "graph.dat" according to a specifies
format. The format's default value is "%lg %lg %lg"
Note that in any of these three cases, SetPoint can be used to change a data
point or add a new one. If the data point index (i) is greater than the
current size of the internal arrays, they are automatically extended.
Specific drawing options can be used to paint a TGraph2D:
"TRI" : The Delaunay triangles are drawn using filled area.
An hidden surface drawing technique is used. The surface is
painted with the current fill area color. The edges of each
triangles are painted with the current line color.
"TRIW" : The Delaunay triangles are drawn as wire frame
"TRI1" : The Delaunay triangles are painted with color levels. The edges
of each triangles are painted with the current line color.
"TRI2" : the Delaunay triangles are painted with color levels.
"P" : Draw a marker at each vertex
"P0" : Draw a circle at each vertex. Each circle background is white.
A TGraph2D can be also drawn with ANY options valid to draw a 2D histogram.
When a TGraph2D is drawn with one of the 2D histogram drawing option,
a intermediate 2D histogram is filled using the Delaunay triangles
technique to interpolate the data set.
TGraph2D linearly interpolate a Z value for any (X,Y) point given some
existing (X,Y,Z) points. The existing (X,Y,Z) points can be randomly
scattered. The algorithm works by joining the existing points to make
Delaunay triangles in (X,Y). These are then used to define flat planes
in (X,Y,Z) over which to interpolate. The interpolated surface thus takes
the form of tessellating triangles at various angles. Output can take the
form of a 2D histogram or a vector. The triangles found can be drawn in 3D.
This software cannot be guaranteed to work under all circumstances. They
were originally written to work with a few hundred points in an XY space
with similar X and Y ranges.
The picture below has been generated by the following macro:
{
TCanvas *c = new TCanvas("c","Graph2D example",0,0,700,600);
Double_t x, y, z, P = 6.;
Int_t np = 200;
TGraph2D *dt = new TGraph2D();
TRandom *r = new TRandom();
for (Int_t N=0; N<np; N++) {
x = 2*P*(r->Rndm(N))-P;
y = 2*P*(r->Rndm(N))-P;
z = (sin(x)/x)*(sin(y)/y)+0.2;
dt->SetPoint(N,x,y,z);
}
gStyle->SetPalette(1);
dt->Draw("surf1");
}
/*
 */
*/
A more complete example can be find in $ROOTSYS/tutorial/graph2dfit.C. It
produces the following output:
/*
 */
*/
Definition of Delaunay triangulation (After B. Delaunay):
For a set S of points in the Euclidean plane, the unique triangulation DT(S)
of S such that no point in S is inside the circumcircle of any triangle in
DT(S). DT(S) is the dual of the Voronoi diagram of S.
If n is the number of points in S, the Voronoi diagram of S is the partitioning
of the plane containing S points into n convex polygons such that each polygon
contains exactly one point and every point in a given polygon is closer to its
central point than to any other. A Voronoi diagram is sometimes also known as
a Dirichlet tessellation.
/*
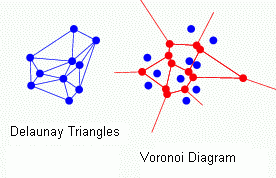
This applet
gives a nice practical view of Delaunay triangulation and Voronoi diagram.
*/
TGraph2D()
: TNamed("Graph2D","Graph2D"), TAttLine(1,1,1), TAttFill(0,1001),
TAttMarker(), fNpoints(0)
Graph2D default constructor
TGraph2D(Int_t n, Int_t *x, Int_t *y, Int_t *z)
: TNamed("Graph2D","Graph2D"), TAttLine(1,1,1), TAttFill(0,1001),
TAttMarker(), fNpoints(n)
Graph2D constructor with three vectors of ints as input.
TGraph2D(Int_t n, Float_t *x, Float_t *y, Float_t *z)
: TNamed("Graph2D","Graph2D"), TAttLine(1,1,1), TAttFill(0,1001),
TAttMarker(), fNpoints(n)
Graph2D constructor with three vectors of floats as input.
TGraph2D(Int_t n, Double_t *x, Double_t *y, Double_t *z)
: TNamed("Graph2D","Graph2D"), TAttLine(1,1,1), TAttFill(0,1001),
TAttMarker(), fNpoints(n)
Graph2D constructor with three vectors of doubles as input.
TGraph2D(TH2 *h2)
: TNamed("Graph2D","Graph2D"), TAttLine(1,1,1), TAttFill(0,1001),
TAttMarker(), fNpoints(0)
Graph2D constructor with a TH2 (h2) as input.
Only the h2's bins within the X and Y axis ranges are used.
TGraph2D(const char *name,const char *title,
Int_t n, Double_t *x, Double_t *y, Double_t *z)
: TNamed(name,title), TAttLine(1,1,1), TAttFill(0,1001),
TAttMarker(), fNpoints(n)
Graph2D constructor with name, title and three vectors of doubles as input.
name : name of 2D graph (avoid blanks)
title : 2D graph title
if title is of the form "stringt;stringx;stringy;stringz"
the 2D graph title is set to stringt, the x axis title to stringy,
the y axis title to stringy,etc
TGraph2D(Int_t n)
: TNamed("Graph2D","Graph2D"), TAttLine(1,1,1), TAttFill(0,1001),
TAttMarker(), fNpoints(0)
Graph2D constructor. The arrays fX, fY and fZ should be filled via
calls to SetPoint
TGraph2D(const char *filename, const char *format, Option_t *)
: TNamed("Graph2D",filename), TAttLine(1,1,1), TAttFill(0,1001),
TAttMarker(), fNpoints(0)
Graph2D constructor reading input from filename
filename is assumed to contain at least three columns of numbers
TGraph2D(const TGraph2D &g)
: TNamed(g), TAttLine(g), TAttFill(g), TAttMarker(g)
Graph2D copy constructor.
~TGraph2D()
TGraph2D destructor.
void Build(Int_t n)
Creates the 2D graph basic data structure
Int_t DistancetoPrimitive(Int_t px, Int_t py)
Computes distance from point px,py to a graph
void Draw(Option_t *option)
Specific drawing options can be used to paint a TGraph2D:
"TRI" : The Delaunay triangles are drawn using filled area.
An hidden surface drawing technique is used. The surface is
painted with the current fill area color. The edges of each
triangles are painted with the current line color.
"TRIW" : The Delaunay triangles are drawn as wire frame
"TRI1" : The Delaunay triangles are painted with color levels. The edges
of each triangles are painted with the current line color.
"TRI2" : the Delaunay triangles are painted with color levels.
"P" : Draw a marker at each vertex
"P0" : Draw a circle at each vertex. Each circle background is white.
A TGraph2D can be also drawn with ANY options valid to draw a 2D histogram.
When a TGraph2D is drawn with one of the 2D histogram drawing option,
a intermediate 2D histogram is filled using the Delaunay triangles
technique to interpolate the data set.
void ExecuteEvent(Int_t event, Int_t px, Int_t py)
Executes action corresponding to one event
TObject* FindObject(const char *name) const
search object named name in the list of functions
TObject* FindObject(const TObject *obj) const
search object obj in the list of functions
Int_t Fit(const char *fname, Option_t *option, Option_t *)
Fits this graph with function with name fname
Int_t Fit(TF2 *f2, Option_t *option, Option_t *)
Fits this 2D graph with function f2
f2 is an already predefined function created by TF2.
Predefined functions such as gaus, expo and poln are automatically
created by ROOT.
The list of fit options is given in parameter option.
option = "W" Set all errors to 1
= "U" Use a User specified fitting algorithm (via SetFCN)
= "Q" Quiet mode (minimum printing)
= "V" Verbose mode (default is between Q and V)
= "R" Use the Range specified in the function range
= "N" Do not store the graphics function, do not draw
= "0" Do not plot the result of the fit. By default the fitted function
is drawn unless the option"N" above is specified.
= "+" Add this new fitted function to the list of fitted functions
(by default, any previous function is deleted)
In order to use the Range option, one must first create a function
with the expression to be fitted. For example, if your graph2d
has a defined range between -4 and 4 and you want to fit a gaussian
only in the interval 1 to 3, you can do:
TF2 *f2 = new TF2("f2","gaus",1,3);
graph2d->Fit("f2","R");
Setting initial conditions
==========================
Parameters must be initialized before invoking the Fit function.
The setting of the parameter initial values is automatic for the
predefined functions : poln, expo, gaus. One can however disable
this automatic computation by specifying the option "B".
You can specify boundary limits for some or all parameters via
f2->SetParLimits(p_number, parmin, parmax);
if parmin>=parmax, the parameter is fixed
Note that you are not forced to fix the limits for all parameters.
For example, if you fit a function with 6 parameters, you can do:
func->SetParameters(0,3.1,1.e-6,0.1,-8,100);
func->SetParLimits(4,-10,-4);
func->SetParLimits(5, 1,1);
With this setup, parameters 0->3 can vary freely
Parameter 4 has boundaries [-10,-4] with initial value -8
Parameter 5 is fixed to 100.
Fit range
=========
The fit range can be specified in two ways:
- specify rxmax > rxmin (default is rxmin=rxmax=0)
- specify the option "R". In this case, the function will be taken
instead of the full graph range.
Changing the fitting function
=============================
By default the fitting function Graph2DFitChisquare is used.
To specify a User defined fitting function, specify option "U" and
call the following functions:
TVirtualFitter::Fitter(mygraph)->SetFCN(MyFittingFunction)
where MyFittingFunction is of type:
extern void MyFittingFunction(Int_t &npar, Double_t *gin, Double_t &f, Double_t *u, Int_t flag);
Associated functions
====================
One or more object (typically a TF2*) can be added to the list
of functions (fFunctions) associated to each graph.
When TGraph::Fit is invoked, the fitted function is added to this list.
Given a graph gr, one can retrieve an associated function
with: TF2 *myfunc = gr->GetFunction("myfunc");
Access to the fit results
=========================
If the graph is made persistent, the list of
associated functions is also persistent. Given a pointer (see above)
to an associated function myfunc, one can retrieve the function/fit
parameters with calls such as:
Double_t chi2 = myfunc->GetChisquare();
Double_t par0 = myfunc->GetParameter(0); //value of 1st parameter
Double_t err0 = myfunc->GetParError(0); //error on first parameter
Fit Statistics
==============
You can change the statistics box to display the fit parameters with
the TStyle::SetOptFit(mode) method. This mode has four digits.
mode = pcev (default = 0111)
v = 1; print name/values of parameters
e = 1; print errors (if e=1, v must be 1)
c = 1; print Chisquare/Number of degress of freedom
p = 1; print Probability
For example: gStyle->SetOptFit(1011);
prints the fit probability, parameter names/values, and errors.
You can change the position of the statistics box with these lines
(where g is a pointer to the TGraph):
Root > TPaveStats *st = (TPaveStats*)g->GetListOfFunctions()->FindObject("stats")
Root > st->SetX1NDC(newx1); //new x start position
Root > st->SetX2NDC(newx2); //new x end position
TAxis* GetXaxis() const
Get x axis of the graph.
TAxis* GetYaxis() const
Get y axis of the graph.
TAxis* GetZaxis() const
Get z axis of the graph.
TList* GetContourList(Double_t contour)
Returns the X and Y graphs building a contour. A contour level may
consist in several parts not connected to each other. This function
returns them in a graphs' list.
Double_t GetErrorX(Int_t) const
This function is called by Graph2DFitChisquare.
It always returns a negative value. Real implementation in TGraph2DErrors
Double_t GetErrorY(Int_t) const
This function is called by Graph2DFitChisquare.
It always returns a negative value. Real implementation in TGraph2DErrors
Double_t GetErrorZ(Int_t) const
This function is called by Graph2DFitChisquare.
It always returns a negative value. Real implementation in TGraph2DErrors
TH2D* GetHistogram(Option_t *option)
By default returns a pointer to the Delaunay histogram. If fHistogram
doesn't exist, books the 2D histogram fHistogram with a margin around
the hull. Calls TGraphDelaunay::Interpolate at each bin centre to build up
an interpolated 2D histogram.
If the "empty" option is selected, returns an empty histogram booked with
the limits of fX, fY and fZ. This option is used when the data set is
drawn with markers only. In that particular case there is no need to
find the Delaunay triangles.
Double_t GetXmax() const
Returns the X maximum
Double_t GetXmin() const
Returns the X minimum
Double_t GetYmax() const
Returns the Y maximum
Double_t GetYmin() const
Returns the Y minimum
Double_t GetZmax() const
Returns the Z maximum
Double_t GetZmin() const
Returns the Z minimum
Double_t Interpolate(Double_t x, Double_t y)
Finds the z value at the position (x,y) thanks to
the Delaunay interpolation.
void Paint(Option_t *option)
Paints this 2D graph with its current attributes
TH1* Project(Option_t *option) const
Projects a 2-d graph into 1 or 2-d histograms depending on the
option parameter
option may contain a combination of the characters x,y,z
option = "x" return the x projection into a TH1D histogram
option = "y" return the y projection into a TH1D histogram
option = "xy" return the x versus y projection into a TH2D histogram
option = "yx" return the y versus x projection into a TH2D histogram
Int_t RemovePoint(Int_t ipoint)
Deletes point number ipoint
void SavePrimitive(ofstream &out, Option_t *option)
Saves primitive as a C++ statement(s) on output stream out
void SetDirectory(TDirectory *dir)
By default when an 2D graph is created, it is added to the list
of 2D graph objects in the current directory in memory.
Remove reference to this 2D graph from current directory and add
reference to new directory dir. dir can be 0 in which case the
2D graph does not belong to any directory.
void SetMargin(Double_t m)
Sets the extra space (in %) around interpolated area for the 2D histogram
void SetMarginBinsContent(Double_t z)
Sets the histogram bin height for points lying outside the TGraphDelaunay
convex hull ie: the bins in the margin.
void SetMaximum(Double_t maximum)
void SetMinimum(Double_t minimum)
void SetName(const char *name)
Changes the name of this 2D graph
void SetNpx(Int_t npx)
Sets the number of bins along X used to draw the function
void SetNpy(Int_t npy)
Sets the number of bins along Y used to draw the function
void SetPoint(Int_t n, Double_t x, Double_t y, Double_t z)
Sets point number n.
If n is greater than the current size, the arrays are automatically
extended.
void SetTitle(const char* title)
Sets graph title
void Streamer(TBuffer &b)
Stream a class object
Inline Functions
TGraph2D operator=(const TGraph2D&)
TDirectory* GetDirectory() const
Int_t GetNpx() const
Int_t GetNpy() const
TList* GetListOfFunctions() const
Double_t GetMargin() const
Int_t GetN() const
Double_t* GetX() const
Double_t* GetY() const
Double_t* GetZ() const
void SetMaxIter(Int_t n = 100000)
TClass* Class()
TClass* IsA() const
void ShowMembers(TMemberInspector& insp, char* parent)
void StreamerNVirtual(TBuffer& b)
Author: Olivier Couet
Last update: root/hist:$Name: $:$Id: TGraph2D.cxx,v 1.00
Copyright (C) 1995-2000, Rene Brun and Fons Rademakers. *
ROOT page - Class index - Class Hierarchy - Top of the page
This page has been automatically generated. If you have any comments or suggestions about the page layout send a mail to ROOT support, or contact the developers with any questions or problems regarding ROOT.
 */
*/
 */
*/
