| mathBeta.C: Test the TMath::BetaDist and TMath::BetaDistI functions | Math tutorials | mathLaplace.C: Test the TMath::LaplaceDist and TMath::LaplaceDistI functions |
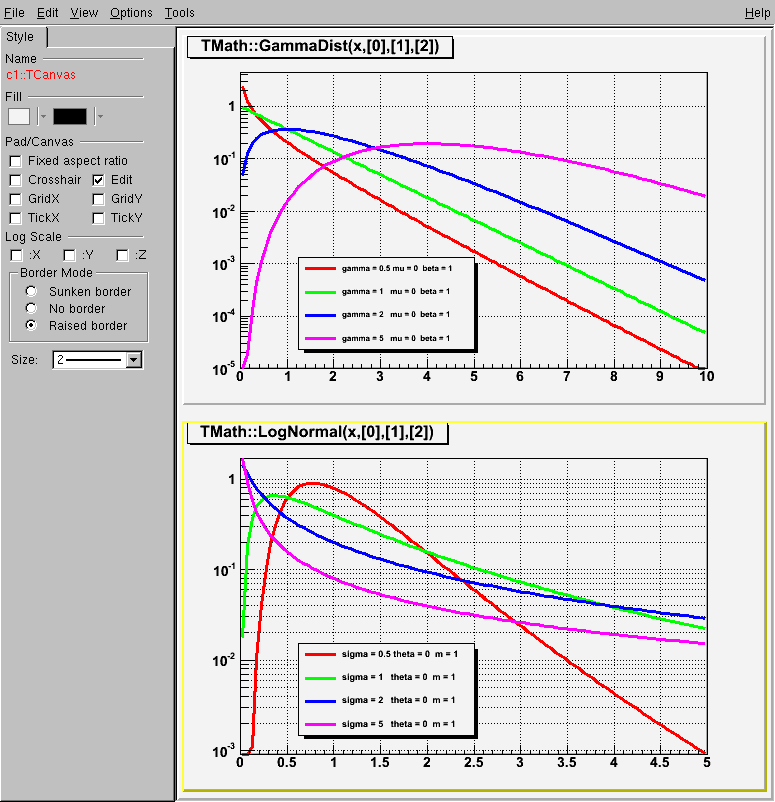
mathGammaNormal.C: tutorial illustrating the use of TMath::GammaDist and TMath::LogNormal
// tutorial illustrating the use of TMath::GammaDist and TMath::LogNormal //Author: Anna Kreshuk void mathGammaNormal(){ TCanvas *myc = new TCanvas("c1","gamma and lognormal",10,10,600,800); myc->Divide(1,2); TPad *pad1 = myc->cd(1); pad1->SetLogy(); pad1->SetGrid(); //TMath::GammaDist TF1 *fgamma = new TF1("fgamma", "TMath::GammaDist(x, [0], [1], [2])", 0, 10); fgamma->SetParameters(0.5, 0, 1); TF1 *f1 = fgamma->DrawCopy(); f1->SetMinimum(1e-5); f1->SetLineColor(kRed); fgamma->SetParameters(1, 0, 1); TF1 *f2 = fgamma->DrawCopy("same"); f2->SetLineColor(kGreen); fgamma->SetParameters(2, 0, 1); TF1 *f3 = fgamma->DrawCopy("same"); f3->SetLineColor(kBlue); fgamma->SetParameters(5, 0, 1); TF1 *f4 = fgamma->DrawCopy("same"); f4->SetLineColor(kMagenta); TLegend *legend1 = new TLegend(.2,.15,.5,.4); legend1->AddEntry(f1,"gamma = 0.5 mu = 0 beta = 1","l"); legend1->AddEntry(f2,"gamma = 1 mu = 0 beta = 1","l"); legend1->AddEntry(f3,"gamma = 2 mu = 0 beta = 1","l"); legend1->AddEntry(f4,"gamma = 5 mu = 0 beta = 1","l"); legend1->Draw(); //TMath::LogNormal TPad *pad2 = myc->cd(2); pad2->SetLogy(); pad2->SetGrid(); TF1 *flog = new TF1("flog", "TMath::LogNormal(x, [0], [1], [2])", 0, 5); flog->SetParameters(0.5, 0, 1); TF1 *g1 = flog->DrawCopy(); g1->SetLineColor(kRed); flog->SetParameters(1, 0, 1); TF1 *g2 = flog->DrawCopy("same"); g2->SetLineColor(kGreen); flog->SetParameters(2, 0, 1); TF1 *g3 = flog->DrawCopy("same"); g3->SetLineColor(kBlue); flog->SetParameters(5, 0, 1); TF1 *g4 = flog->DrawCopy("same"); g4->SetLineColor(kMagenta); TLegend *legend2 = new TLegend(.2,.15,.5,.4); legend2->AddEntry(g1,"sigma = 0.5 theta = 0 m = 1","l"); legend2->AddEntry(g2,"sigma = 1 theta = 0 m = 1","l"); legend2->AddEntry(g3,"sigma = 2 theta = 0 m = 1","l"); legend2->AddEntry(g4,"sigma = 5 theta = 0 m = 1","l"); legend2->Draw(); } mathGammaNormal.C:1 mathGammaNormal.C:2 mathGammaNormal.C:3 mathGammaNormal.C:4 mathGammaNormal.C:5 mathGammaNormal.C:6 mathGammaNormal.C:7 mathGammaNormal.C:8 mathGammaNormal.C:9 mathGammaNormal.C:10 mathGammaNormal.C:11 mathGammaNormal.C:12 mathGammaNormal.C:13 mathGammaNormal.C:14 mathGammaNormal.C:15 mathGammaNormal.C:16 mathGammaNormal.C:17 mathGammaNormal.C:18 mathGammaNormal.C:19 mathGammaNormal.C:20 mathGammaNormal.C:21 mathGammaNormal.C:22 mathGammaNormal.C:23 mathGammaNormal.C:24 mathGammaNormal.C:25 mathGammaNormal.C:26 mathGammaNormal.C:27 mathGammaNormal.C:28 mathGammaNormal.C:29 mathGammaNormal.C:30 mathGammaNormal.C:31 mathGammaNormal.C:32 mathGammaNormal.C:33 mathGammaNormal.C:34 mathGammaNormal.C:35 mathGammaNormal.C:36 mathGammaNormal.C:37 mathGammaNormal.C:38 mathGammaNormal.C:39 mathGammaNormal.C:40 mathGammaNormal.C:41 mathGammaNormal.C:42 mathGammaNormal.C:43 mathGammaNormal.C:44 mathGammaNormal.C:45 mathGammaNormal.C:46 mathGammaNormal.C:47 mathGammaNormal.C:48 mathGammaNormal.C:49 mathGammaNormal.C:50 mathGammaNormal.C:51 mathGammaNormal.C:52 mathGammaNormal.C:53 mathGammaNormal.C:54 mathGammaNormal.C:55 mathGammaNormal.C:56 mathGammaNormal.C:57 |
|