| fitslicesy.C: Illustrates how to use the TH1::FitSlicesY function | Fitting tutorials | langaus.C: Convoluted Landau and Gaussian Fitting Function |
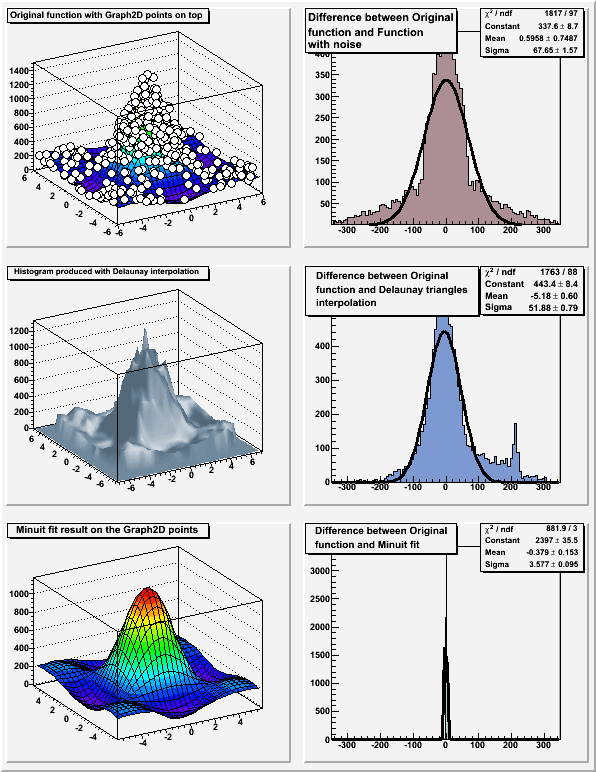
graph2dfit.C: Fitting a TGraph2D
//Fitting a TGraph2D //Author: Olivier Couet #include <TMath.h> #include <TGraph2D.h> #include <TRandom.h> #include <TStyle.h> #include <TCanvas.h> #include <TF2.h> #include <TH1.h> TCanvas* graph2dfit() { gStyle->SetOptStat(0); gStyle->SetOptFit(); TCanvas *c = new TCanvas("c","Graph2D example",0,0,600,800); c->Divide(2,3); Double_t rnd, x, y, z; Double_t e = 0.3; Int_t nd = 400; Int_t np = 10000; TRandom r; Double_t fl = 6; TF2 *f2 = new TF2("f2","1000*(([0]*sin(x)/x)*([1]*sin(y)/y))+200", -fl,fl,-fl,fl); f2->SetParameters(1,1); TGraph2D *dt = new TGraph2D(); // Fill the 2D graph Double_t zmax = 0; for (Int_t N=0; N<nd; N++) { f2->GetRandom2(x,y); // Generate a random number in [-e,e] rnd = 2*r.Rndm()*e-e; z = f2->Eval(x,y)*(1+rnd); if (z>zmax) zmax = z; dt->SetPoint(N,x,y,z); } Double_t hr = 350; TH1D *h1 = new TH1D("h1", "#splitline{Difference between Original}{#splitline{function and Function}{with noise}}", 100, -hr, hr); TH1D *h2 = new TH1D("h2", "#splitline{Difference between Original}{#splitline{function and Delaunay triangles}{interpolation}}", 100, -hr, hr); TH1D *h3 = new TH1D("h3", "#splitline{Difference between Original}{function and Minuit fit}", 500, -hr, hr); f2->SetParameters(0.5,1.5); dt->Fit(f2); TF2 *fit2 = (TF2*)dt->FindObject("f2"); f2->SetParameters(1,1); for (Int_t N=0; N<np; N++) { f2->GetRandom2(x,y); // Generate a random number in [-e,e] rnd = 2*r.Rndm()*e-e; z = f2->Eval(x,y)*(1+rnd); h1->Fill(f2->Eval(x,y)-z); z = dt->Interpolate(x,y); h2->Fill(f2->Eval(x,y)-z); z = fit2->Eval(x,y); h3->Fill(f2->Eval(x,y)-z); } gStyle->SetPalette(1); c->cd(1); f2->SetTitle("Original function with Graph2D points on top"); f2->SetMaximum(zmax); gStyle->SetHistTopMargin(0); f2->Draw("surf1"); dt->Draw("same p0"); c->cd(3); dt->SetMargin(0.1); dt->SetFillColor(36); dt->SetTitle("Histogram produced with Delaunay interpolation"); dt->Draw("surf4"); c->cd(5); fit2->SetTitle("Minuit fit result on the Graph2D points"); fit2->Draw("surf1"); h1->SetFillColor(47); h2->SetFillColor(38); h3->SetFillColor(29); c->cd(2); h1->Fit("gaus","Q") ; h1->Draw(); c->cd(4); h2->Fit("gaus","Q") ; h2->Draw(); c->cd(6); h3->Fit("gaus","Q") ; h3->Draw(); c->cd(); return c; } graph2dfit.C:1 graph2dfit.C:2 graph2dfit.C:3 graph2dfit.C:4 graph2dfit.C:5 graph2dfit.C:6 graph2dfit.C:7 graph2dfit.C:8 graph2dfit.C:9 graph2dfit.C:10 graph2dfit.C:11 graph2dfit.C:12 graph2dfit.C:13 graph2dfit.C:14 graph2dfit.C:15 graph2dfit.C:16 graph2dfit.C:17 graph2dfit.C:18 graph2dfit.C:19 graph2dfit.C:20 graph2dfit.C:21 graph2dfit.C:22 graph2dfit.C:23 graph2dfit.C:24 graph2dfit.C:25 graph2dfit.C:26 graph2dfit.C:27 graph2dfit.C:28 graph2dfit.C:29 graph2dfit.C:30 graph2dfit.C:31 graph2dfit.C:32 graph2dfit.C:33 graph2dfit.C:34 graph2dfit.C:35 graph2dfit.C:36 graph2dfit.C:37 graph2dfit.C:38 graph2dfit.C:39 graph2dfit.C:40 graph2dfit.C:41 graph2dfit.C:42 graph2dfit.C:43 graph2dfit.C:44 graph2dfit.C:45 graph2dfit.C:46 graph2dfit.C:47 graph2dfit.C:48 graph2dfit.C:49 graph2dfit.C:50 graph2dfit.C:51 graph2dfit.C:52 graph2dfit.C:53 graph2dfit.C:54 graph2dfit.C:55 graph2dfit.C:56 graph2dfit.C:57 graph2dfit.C:58 graph2dfit.C:59 graph2dfit.C:60 graph2dfit.C:61 graph2dfit.C:62 graph2dfit.C:63 graph2dfit.C:64 graph2dfit.C:65 graph2dfit.C:66 graph2dfit.C:67 graph2dfit.C:68 graph2dfit.C:69 graph2dfit.C:70 graph2dfit.C:71 graph2dfit.C:72 graph2dfit.C:73 graph2dfit.C:74 graph2dfit.C:75 graph2dfit.C:76 graph2dfit.C:77 graph2dfit.C:78 graph2dfit.C:79 graph2dfit.C:80 graph2dfit.C:81 graph2dfit.C:82 graph2dfit.C:83 graph2dfit.C:84 graph2dfit.C:85 graph2dfit.C:86 graph2dfit.C:87 graph2dfit.C:88 graph2dfit.C:89 graph2dfit.C:90 graph2dfit.C:91 graph2dfit.C:92 graph2dfit.C:93 graph2dfit.C:94 graph2dfit.C:95 graph2dfit.C:96 graph2dfit.C:97 graph2dfit.C:98 graph2dfit.C:99 graph2dfit.C:100 |
|