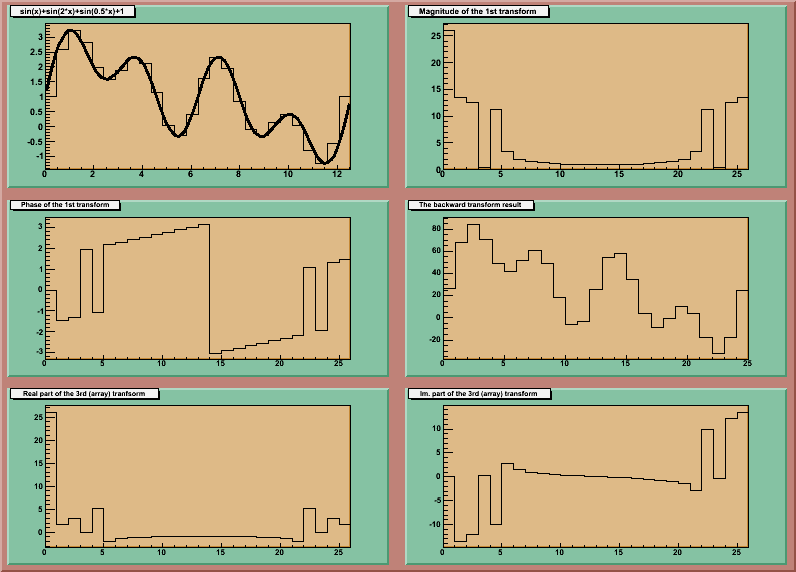
FFT.C: This tutorial illustrates the Fast Fourier Transforms interface in ROOT.
#include "TH1D.h" #include "TVirtualFFT.h" #include "TF1.h" #include "TCanvas.h" #include "TMath.h" void FFT() { //This tutorial illustrates the Fast Fourier Transforms interface in ROOT. //FFT transform types provided in ROOT: // - "C2CFORWARD" - a complex input/output discrete Fourier transform (DFT) // in one or more dimensions, -1 in the exponent // - "C2CBACKWARD"- a complex input/output discrete Fourier transform (DFT) // in one or more dimensions, +1 in the exponent // - "R2C" - a real-input/complex-output discrete Fourier transform (DFT) // in one or more dimensions, // - "C2R" - inverse transforms to "R2C", taking complex input // (storing the non-redundant half of a logically Hermitian array) // to real output // - "R2HC" - a real-input DFT with output in ¡Èhalfcomplex¡É format, // i.e. real and imaginary parts for a transform of size n stored as // r0, r1, r2, ..., rn/2, i(n+1)/2-1, ..., i2, i1 // - "HC2R" - computes the reverse of FFTW_R2HC, above // - "DHT" - computes a discrete Hartley transform // Sine/cosine transforms: // DCT-I (REDFT00 in FFTW3 notation) // DCT-II (REDFT10 in FFTW3 notation) // DCT-III(REDFT01 in FFTW3 notation) // DCT-IV (REDFT11 in FFTW3 notation) // DST-I (RODFT00 in FFTW3 notation) // DST-II (RODFT10 in FFTW3 notation) // DST-III(RODFT01 in FFTW3 notation) // DST-IV (RODFT11 in FFTW3 notation) //First part of the tutorial shows how to transform the histograms //Second part shows how to transform the data arrays directly //Authors: Anna Kreshuk and Jens Hoffmann //********* Histograms ********// //prepare the canvas for drawing TCanvas *myc = new TCanvas("myc", "Fast Fourier Transform", 800, 600); myc->SetFillColor(45); TPad *c1_1 = new TPad("c1_1", "c1_1",0.01,0.67,0.49,0.99); TPad *c1_2 = new TPad("c1_2", "c1_2",0.51,0.67,0.99,0.99); TPad *c1_3 = new TPad("c1_3", "c1_3",0.01,0.34,0.49,0.65); TPad *c1_4 = new TPad("c1_4", "c1_4",0.51,0.34,0.99,0.65); TPad *c1_5 = new TPad("c1_5", "c1_5",0.01,0.01,0.49,0.32); TPad *c1_6 = new TPad("c1_6", "c1_6",0.51,0.01,0.99,0.32); c1_1->Draw(); c1_2->Draw(); c1_3->Draw(); c1_4->Draw(); c1_5->Draw(); c1_6->Draw(); c1_1->SetFillColor(30); c1_1->SetFrameFillColor(42); c1_2->SetFillColor(30); c1_2->SetFrameFillColor(42); c1_3->SetFillColor(30); c1_3->SetFrameFillColor(42); c1_4->SetFillColor(30); c1_4->SetFrameFillColor(42); c1_5->SetFillColor(30); c1_5->SetFrameFillColor(42); c1_6->SetFillColor(30); c1_6->SetFrameFillColor(42); c1_1->cd(); TH1::AddDirectory(kFALSE); //A function to sample TF1 *fsin = new TF1("fsin", "sin(x)+sin(2*x)+sin(0.5*x)+1", 0, 4*TMath::Pi()); fsin->Draw(); Int_t n=25; TH1D *hsin = new TH1D("hsin", "hsin", n+1, 0, 4*TMath::Pi()); Double_t x; //Fill the histogram with function values for (Int_t i=0; i<=n; i++){ x = (Double_t(i)/n)*(4*TMath::Pi()); hsin->SetBinContent(i+1, fsin->Eval(x)); } hsin->Draw("same"); fsin->GetXaxis()->SetLabelSize(0.05); fsin->GetYaxis()->SetLabelSize(0.05); c1_2->cd(); //Compute the transform and look at the magnitude of the output TH1 *hm =0; TVirtualFFT::SetTransform(0); hm = hsin->FFT(hm, "MAG"); hm->SetTitle("Magnitude of the 1st transform"); hm->Draw(); //NOTE: for "real" frequencies you have to divide the x-axes range with the range of your function //(in this case 4*Pi); y-axes has to be rescaled by a factor of 1/SQRT(n) to be right: this is not done automatically! hm->SetStats(kFALSE); hm->GetXaxis()->SetLabelSize(0.05); hm->GetYaxis()->SetLabelSize(0.05); c1_3->cd(); //Look at the phase of the output TH1 *hp = 0; hp = hsin->FFT(hp, "PH"); hp->SetTitle("Phase of the 1st transform"); hp->Draw(); hp->SetStats(kFALSE); hp->GetXaxis()->SetLabelSize(0.05); hp->GetYaxis()->SetLabelSize(0.05); //Look at the DC component and the Nyquist harmonic: Double_t re, im; //That's the way to get the current transform object: TVirtualFFT *fft = TVirtualFFT::GetCurrentTransform(); c1_4->cd(); //Use the following method to get just one point of the output fft->GetPointComplex(0, re, im); printf("1st transform: DC component: %f\n", re); fft->GetPointComplex(n/2+1, re, im); printf("1st transform: Nyquist harmonic: %f\n", re); //Use the following method to get the full output: Double_t *re_full = new Double_t[n]; Double_t *im_full = new Double_t[n]; fft->GetPointsComplex(re_full,im_full); //Now let's make a backward transform: TVirtualFFT *fft_back = TVirtualFFT::FFT(1, &n, "C2R M K"); fft_back->SetPointsComplex(re_full,im_full); fft_back->Transform(); TH1 *hb = 0; //Let's look at the output hb = TH1::TransformHisto(fft_back,hb,"Re"); hb->SetTitle("The backward transform result"); hb->Draw(); //NOTE: here you get at the x-axes number of bins and not real values //(in this case 25 bins has to be rescaled to a range between 0 and 4*Pi; //also here the y-axes has to be rescaled (factor 1/bins) hb->SetStats(kFALSE); hb->GetXaxis()->SetLabelSize(0.05); hb->GetYaxis()->SetLabelSize(0.05); delete fft_back; fft_back=0; //********* Data array - same transform ********// //Allocate an array big enough to hold the transform output //Transform output in 1d contains, for a transform of size N, //N/2+1 complex numbers, i.e. 2*(N/2+1) real numbers //our transform is of size n+1, because the histogram has n+1 bins Double_t *in = new Double_t[2*((n+1)/2+1)]; Double_t re_2,im_2; for (Int_t i=0; i<=n; i++){ x = (Double_t(i)/n)*(4*TMath::Pi()); in[i] = fsin->Eval(x); } //Make our own TVirtualFFT object (using option "K") //Third parameter (option) consists of 3 parts: //-transform type: // real input/complex output in our case //-transform flag: // the amount of time spent in planning // the transform (see TVirtualFFT class description) //-to create a new TVirtualFFT object (option "K") or use the global (default) Int_t n_size = n+1; TVirtualFFT *fft_own = TVirtualFFT::FFT(1, &n_size, "R2C ES K"); if (!fft_own) return; fft_own->SetPoints(in); fft_own->Transform(); //Copy all the output points: fft_own->GetPoints(in); //Draw the real part of the output c1_5->cd(); TH1 *hr = 0; hr = TH1::TransformHisto(fft_own, hr, "RE"); hr->SetTitle("Real part of the 3rd (array) tranfsorm"); hr->Draw(); hr->SetStats(kFALSE); hr->GetXaxis()->SetLabelSize(0.05); hr->GetYaxis()->SetLabelSize(0.05); c1_6->cd(); TH1 *him = 0; him = TH1::TransformHisto(fft_own, him, "IM"); him->SetTitle("Im. part of the 3rd (array) transform"); him->Draw(); him->SetStats(kFALSE); him->GetXaxis()->SetLabelSize(0.05); him->GetYaxis()->SetLabelSize(0.05); myc->cd(); //Now let's make another transform of the same size //The same transform object can be used, as the size and the type of the transform //haven't changed TF1 *fcos = new TF1("fcos", "cos(x)+cos(0.5*x)+cos(2*x)+1", 0, 4*TMath::Pi()); for (Int_t i=0; i<=n; i++){ x = (Double_t(i)/n)*(4*TMath::Pi()); in[i] = fcos->Eval(x); } fft_own->SetPoints(in); fft_own->Transform(); fft_own->GetPointComplex(0, re_2, im_2); printf("2nd transform: DC component: %f\n", re_2); fft_own->GetPointComplex(n/2+1, re_2, im_2); printf("2nd transform: Nyquist harmonic: %f\n", re_2); delete fft_own; delete [] in; delete [] re_full; delete [] im_full; } FFT.C:1 FFT.C:2 FFT.C:3 FFT.C:4 FFT.C:5 FFT.C:6 FFT.C:7 FFT.C:8 FFT.C:9 FFT.C:10 FFT.C:11 FFT.C:12 FFT.C:13 FFT.C:14 FFT.C:15 FFT.C:16 FFT.C:17 FFT.C:18 FFT.C:19 FFT.C:20 FFT.C:21 FFT.C:22 FFT.C:23 FFT.C:24 FFT.C:25 FFT.C:26 FFT.C:27 FFT.C:28 FFT.C:29 FFT.C:30 FFT.C:31 FFT.C:32 FFT.C:33 FFT.C:34 FFT.C:35 FFT.C:36 FFT.C:37 FFT.C:38 FFT.C:39 FFT.C:40 FFT.C:41 FFT.C:42 FFT.C:43 FFT.C:44 FFT.C:45 FFT.C:46 FFT.C:47 FFT.C:48 FFT.C:49 FFT.C:50 FFT.C:51 FFT.C:52 FFT.C:53 FFT.C:54 FFT.C:55 FFT.C:56 FFT.C:57 FFT.C:58 FFT.C:59 FFT.C:60 FFT.C:61 FFT.C:62 FFT.C:63 FFT.C:64 FFT.C:65 FFT.C:66 FFT.C:67 FFT.C:68 FFT.C:69 FFT.C:70 FFT.C:71 FFT.C:72 FFT.C:73 FFT.C:74 FFT.C:75 FFT.C:76 FFT.C:77 FFT.C:78 FFT.C:79 FFT.C:80 FFT.C:81 FFT.C:82 FFT.C:83 FFT.C:84 FFT.C:85 FFT.C:86 FFT.C:87 FFT.C:88 FFT.C:89 FFT.C:90 FFT.C:91 FFT.C:92 FFT.C:93 FFT.C:94 FFT.C:95 FFT.C:96 FFT.C:97 FFT.C:98 FFT.C:99 FFT.C:100 FFT.C:101 FFT.C:102 FFT.C:103 FFT.C:104 FFT.C:105 FFT.C:106 FFT.C:107 FFT.C:108 FFT.C:109 FFT.C:110 FFT.C:111 FFT.C:112 FFT.C:113 FFT.C:114 FFT.C:115 FFT.C:116 FFT.C:117 FFT.C:118 FFT.C:119 FFT.C:120 FFT.C:121 FFT.C:122 FFT.C:123 FFT.C:124 FFT.C:125 FFT.C:126 FFT.C:127 FFT.C:128 FFT.C:129 FFT.C:130 FFT.C:131 FFT.C:132 FFT.C:133 FFT.C:134 FFT.C:135 FFT.C:136 FFT.C:137 FFT.C:138 FFT.C:139 FFT.C:140 FFT.C:141 FFT.C:142 FFT.C:143 FFT.C:144 FFT.C:145 FFT.C:146 FFT.C:147 FFT.C:148 FFT.C:149 FFT.C:150 FFT.C:151 FFT.C:152 FFT.C:153 FFT.C:154 FFT.C:155 FFT.C:156 FFT.C:157 FFT.C:158 FFT.C:159 FFT.C:160 FFT.C:161 FFT.C:162 FFT.C:163 FFT.C:164 FFT.C:165 FFT.C:166 FFT.C:167 FFT.C:168 FFT.C:169 FFT.C:170 FFT.C:171 FFT.C:172 FFT.C:173 FFT.C:174 FFT.C:175 FFT.C:176 FFT.C:177 FFT.C:178 FFT.C:179 FFT.C:180 FFT.C:181 FFT.C:182 FFT.C:183 FFT.C:184 FFT.C:185 FFT.C:186 FFT.C:187 FFT.C:188 FFT.C:189 FFT.C:190 FFT.C:191 FFT.C:192 FFT.C:193 FFT.C:194 FFT.C:195 FFT.C:196 FFT.C:197 FFT.C:198 FFT.C:199 FFT.C:200 FFT.C:201 FFT.C:202 FFT.C:203 FFT.C:204 FFT.C:205 FFT.C:206 FFT.C:207 FFT.C:208 FFT.C:209 FFT.C:210 FFT.C:211 FFT.C:212 FFT.C:213 FFT.C:214 FFT.C:215 FFT.C:216 FFT.C:217 |
|