rf102_dataimport.C File Reference

Detailed Description

'BASIC FUNCTIONALITY' RooFit tutorial macro #102

Importing data from ROOT TTrees and THx histograms

 
 
␛[1mRooFit v3.60 -- Developed by Wouter Verkerke and David Kirkby␛[0m 
                Copyright (C) 2000-2013 NIKHEF, University of California & Stanford University
                All rights reserved, please read http://roofit.sourceforge.net/license.txt
 
[#1] INFO:Minization -- RooMinimizer::optimizeConst: activating const optimization
 **********
 **    1 **SET PRINT           1
 **********
 **********
 **    2 **SET NOGRAD
 **********
 PARAMETER DEFINITIONS:
    NO.   NAME         VALUE      STEP SIZE      LIMITS
     1 mean         0.00000e+00  2.00000e+00   -1.00000e+01  1.00000e+01
     2 sigma        3.00000e+00  9.90000e-01    1.00000e-01  1.00000e+01
 **********
 **    3 **SET ERR         0.5
 **********
 **********
 **    4 **SET PRINT           1
 **********
 **********
 **    5 **SET STR           1
 **********
 NOW USING STRATEGY  1: TRY TO BALANCE SPEED AGAINST RELIABILITY
 **********
 **    6 **MIGRAD        1000           1
 **********
 FIRST CALL TO USER FUNCTION AT NEW START POINT, WITH IFLAG=4.
 START MIGRAD MINIMIZATION.  STRATEGY  1.  CONVERGENCE WHEN EDM .LT. 1.00e-03
 FCN=249.349 FROM MIGRAD    STATUS=INITIATE        8 CALLS           9 TOTAL
                     EDM= unknown      STRATEGY= 1      NO ERROR MATRIX       
  EXT PARAMETER               CURRENT GUESS       STEP         FIRST   
  NO.   NAME      VALUE            ERROR          SIZE      DERIVATIVE 
   1  mean         0.00000e+00   2.00000e+00   2.01358e-01   1.15556e+01
   2  sigma        3.00000e+00   9.90000e-01   2.22742e-01   5.42294e+00
                               ERR DEF= 0.5
 MIGRAD MINIMIZATION HAS CONVERGED.
 MIGRAD WILL VERIFY CONVERGENCE AND ERROR MATRIX.
 COVARIANCE MATRIX CALCULATED SUCCESSFULLY
 FCN=249.251 FROM MIGRAD    STATUS=CONVERGED      23 CALLS          24 TOTAL
                     EDM=1.58964e-05    STRATEGY= 1      ERROR MATRIX ACCURATE 
  EXT PARAMETER                                   STEP         FIRST   
  NO.   NAME      VALUE            ERROR          SIZE      DERIVATIVE 
   1  mean        -1.05079e-01   2.95122e-01   3.29083e-04  -2.34747e-02
   2  sigma        2.93926e+00   2.13363e-01   5.44955e-04  -8.23858e-02
                               ERR DEF= 0.5
 EXTERNAL ERROR MATRIX.    NDIM=  25    NPAR=  2    ERR DEF=0.5
  8.712e-02 -9.823e-05 
 -9.823e-05  4.556e-02 
 PARAMETER  CORRELATION COEFFICIENTS  
       NO.  GLOBAL      1      2
        1  0.00156   1.000 -0.002
        2  0.00156  -0.002  1.000
 **********
 **    7 **SET ERR         0.5
 **********
 **********
 **    8 **SET PRINT           1
 **********
 **********
 **    9 **HESSE        1000
 **********
 COVARIANCE MATRIX CALCULATED SUCCESSFULLY
 FCN=249.251 FROM HESSE     STATUS=OK             10 CALLS          34 TOTAL
                     EDM=1.58906e-05    STRATEGY= 1      ERROR MATRIX ACCURATE 
  EXT PARAMETER                                INTERNAL      INTERNAL  
  NO.   NAME      VALUE            ERROR       STEP SIZE       VALUE   
   1  mean        -1.05079e-01   2.95122e-01   6.58167e-05  -1.05081e-02
   2  sigma        2.93926e+00   2.13363e-01   1.08991e-04  -4.40523e-01
                               ERR DEF= 0.5
 EXTERNAL ERROR MATRIX.    NDIM=  25    NPAR=  2    ERR DEF=0.5
  8.712e-02 -1.406e-04 
 -1.406e-04  4.556e-02 
 PARAMETER  CORRELATION COEFFICIENTS  
       NO.  GLOBAL      1      2
        1  0.00223   1.000 -0.002
        2  0.00223  -0.002  1.000
[#1] INFO:Minization -- RooMinimizer::optimizeConst: deactivating const optimization
[#1] INFO:Eval -- RooTreeDataStore::loadValues(ds) Ignored 36 out of range events
 
-----------------------
Reading data from ASCII
[#1] INFO:DataHandling -- RooDataSet::read: reading file /tmp/rf102_testData.txt
[#0] ERROR:DataHandling -- RooDataSet::read(static): read error at line 65
[#1] INFO:DataHandling -- RooDataSet::read: read 64 events (ignored 0 out of range events)
DataStore dataset (/tmp/rf102_testData.txt)
  Contains 64 entries
  Observables: 
    1)           x = 0.0174204  L(-10 - 10)  "x"
    2)           y = 9.46654  L(-10 - 10)  "y"
    3)  blindState = Normal(idx = 0)
  "Blinding State"
 
Original data, line 20:
  1) RooRealVar:: x = -0.79919
  2) RooRealVar:: y = 0.0106407
 
Read-back data, line 20:
  1) RooRealVar::          x = -0.79919
  2) RooRealVar::          y = 0.0106407
  3) RooCategory:: blindState = Normal(idx = 0)
 
RooDataSet::ds[x,y] = 64 entries

 
 
#include "RooRealVar.h"
#include "RooDataSet.h"
#include "RooDataHist.h"
#include "RooGaussian.h"
#include "TCanvas.h"
#include "RooPlot.h"
#include "TTree.h"
#include "TH1D.h"
#include "TRandom.h"
using namespace RooFit ;
 
TH1* makeTH1() ;
TTree* makeTTree() ;
 
 
void rf102_dataimport()
{
   // ---------------------------------------------------
   // I m p o r t i n g   R O O T   h i s t o g r a m s 
   // ===================================================
 
   // I m p o r t   T H 1   i n t o   a   R o o D a t a H i s t
   // ---------------------------------------------------------
 
   // Create a ROOT TH1 histogram
   TH1* hh = makeTH1() ;
 
   // Declare observable x
   RooRealVar x("x","x",-10,10) ;
 
   // Create a binned dataset that imports contents of TH1 and associates its contents to observable 'x'
   RooDataHist dh("dh","dh",x,Import(*hh)) ;
 
 
   // P l o t   a n d   f i t   a   R o o D a t a H i s t
   // ---------------------------------------------------
 
   // Make plot of binned dataset showing Poisson error bars (RooFit default)
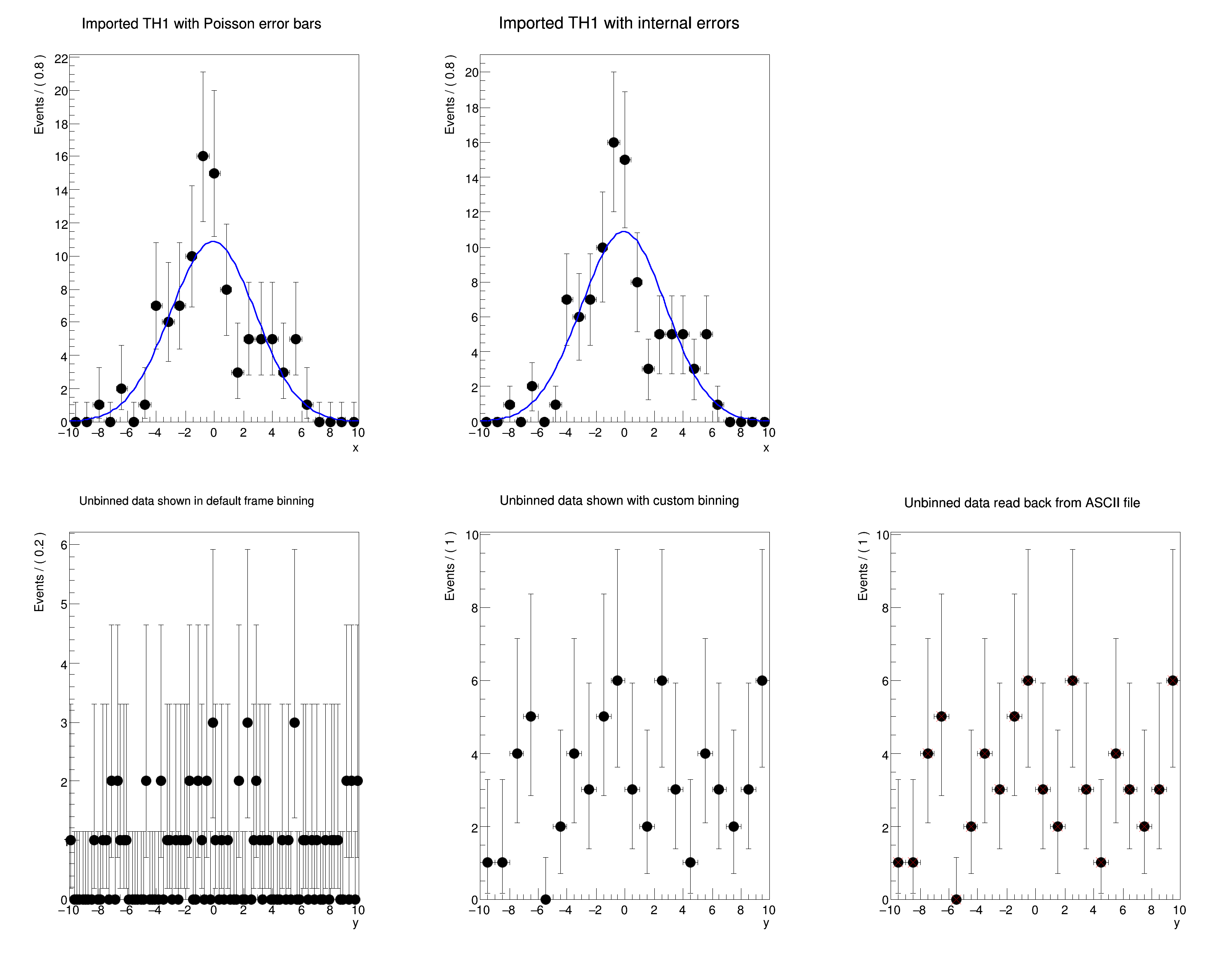
   RooPlot* frame = x.frame(Title("Imported TH1 with Poisson error bars")) ;
   dh.plotOn(frame) ; 
 
   // Fit a Gaussian p.d.f to the data
   RooRealVar mean("mean","mean",0,-10,10) ;
   RooRealVar sigma("sigma","sigma",3,0.1,10) ;
   RooGaussian gauss("gauss","gauss",x,mean,sigma) ;
   gauss.fitTo(dh) ;
   gauss.plotOn(frame) ;
 
   // P l o t   a n d   f i t   a   R o o D a t a H i s t   w i t h   i n t e r n a l   e r r o r s
   // ---------------------------------------------------------------------------------------------
 
   // If histogram has custom error (i.e. its contents is does not originate from a Poisson process
   // but e.g. is a sum of weighted events) you can data with symmetric 'sum-of-weights' error instead
   // (same error bars as shown by ROOT)
   RooPlot* frame2 = x.frame(Title("Imported TH1 with internal errors")) ;
   dh.plotOn(frame2,DataError(RooAbsData::SumW2)) ; 
   gauss.plotOn(frame2) ;
 
   // Please note that error bars shown (Poisson or SumW2) are for visualization only, the are NOT used
   // in a maximum likelihood fit
   //
   // A (binned) ML fit will ALWAYS assume the Poisson error interpretation of data (the mathematical definition 
   // of likelihood does not take any external definition of errors). Data with non-unit weights can only be correctly
   // fitted with a chi^2 fit (see rf602_chi2fit.C) 
 
 
   // -----------------------------------------
   // I m p o r t i n g   R O O T  T T r e e s
   // =========================================
 
 
   // I m p o r t   T T r e e   i n t o   a   R o o D a t a S e t
   // -----------------------------------------------------------
 
   TTree* tree = makeTTree() ;
 
   // Define 2nd observable y
   RooRealVar y("y","y",-10,10) ;
 
   // Construct unbinned dataset importing tree branches x and y matching between branches and RooRealVars 
   // is done by name of the branch/RRV 
   // 
   // Note that ONLY entries for which x,y have values within their allowed ranges as defined in 
   // RooRealVar x and y are imported. Since the y values in the import tree are in the range [-15,15]
   // and RRV y defines a range [-10,10] this means that the RooDataSet below will have less entries than the TTree 'tree'
 
   RooDataSet ds("ds","ds",RooArgSet(x,y),Import(*tree)) ;
   
   
   
   // U s e   a s c i i   i m p o r t / e x p o r t   f o r   d a t a s e t s
   // ------------------------------------------------------------------------------------
   {
      // Write data to output stream
      std::ofstream outstream("/tmp/rf102_testData.txt");
      // Optionally, adjust the stream here (e.g. std::setprecision)
      ds.write(outstream);
      outstream.close();
   }
   
     
   //Read data from input stream. The variables of the dataset need to be supplied
   //to the RooDataSet::read() function.
   std::cout << "\n-----------------------\nReading data from ASCII\n";
   RooDataSet * dataReadBack = RooDataSet::read("/tmp/rf102_testData.txt",
      RooArgList(x, y), //variables to be read. If the file has more fields, these are ignored.
      "D"); //Prints if a RooFit message stream listens for debug messages. Use Q for quiet.
   
   dataReadBack->Print("V");
   
   std::cout << "\nOriginal data, line 20:\n";
   ds.get(20)->Print("V");
   
   std::cout << "\nRead-back data, line 20:\n";
   dataReadBack->get(20)->Print("V");
 
 
 
   // P l o t   d a t a s e t s  w i t h   m u l t i p l e   b i n n i n g   c h o i c e s
   // ------------------------------------------------------------------------------------
 
   // Print number of events in dataset
   ds.Print() ;
 
   // Print unbinned dataset with default frame binning (100 bins)
   RooPlot* frame3 = y.frame(Title("Unbinned data shown in default frame binning")) ;
   ds.plotOn(frame3) ;
 
   // Print unbinned dataset with custom binning choice (20 bins)
   RooPlot* frame4 = y.frame(Title("Unbinned data shown with custom binning")) ;
   ds.plotOn(frame4,Binning(20)) ;
 
   RooPlot* frame5 = y.frame(Title("Unbinned data read back from ASCII file")) ;
   ds.plotOn(frame5,Binning(20)) ;
   dataReadBack->plotOn(frame5, Binning(20), MarkerColor(kRed), MarkerStyle(5));
   
   // Draw all frames on a canvas
   TCanvas* c = new TCanvas("rf102_dataimport","rf102_dataimport",1000,800) ;
   c->Divide(3,2) ;
   c->cd(1) ; gPad->SetLeftMargin(0.15) ; frame->GetYaxis()->SetTitleOffset(1.4) ; frame->Draw() ;
   c->cd(2) ; gPad->SetLeftMargin(0.15) ; frame2->GetYaxis()->SetTitleOffset(1.4) ; frame2->Draw() ;
   
   c->cd(4) ; gPad->SetLeftMargin(0.15) ; frame3->GetYaxis()->SetTitleOffset(1.4) ; frame3->Draw() ;
   c->cd(5) ; gPad->SetLeftMargin(0.15) ; frame4->GetYaxis()->SetTitleOffset(1.4) ; frame4->Draw() ;
   c->cd(6) ; gPad->SetLeftMargin(0.15) ; frame4->GetYaxis()->SetTitleOffset(1.4) ; frame5->Draw() ;
 
}
 
 
 
 
TH1* makeTH1() 
{
   // Create ROOT TH1 filled with a Gaussian distribution
 
   TH1D* hh = new TH1D("hh","hh",25,-10,10) ;
   for (int i=0 ; i<100 ; i++) {
      hh->Fill(gRandom->Gaus(0,3)) ;
   }
   return hh ;
}
 
 
TTree* makeTTree() 
{
  // Create ROOT TTree filled with a Gaussian distribution in x and a uniform distribution in y
 
  TTree* tree = new TTree("tree","tree") ;
  Double_t* px = new Double_t ;
  Double_t* py = new Double_t ;
  tree->Branch("x",px,"x/D") ;
  tree->Branch("y",py,"y/D") ;
  for (int i=0 ; i<100 ; i++) {
    *px = gRandom->Gaus(0,3) ;
    *py = gRandom->Uniform()*30 - 15 ;
    tree->Fill() ;
  }
  return tree ;
}
 
 

Author

07/2008 - Wouter Verkerke

Definition in file rf102_dataimport.C.