Logo ROOT   6.16/01
Reference Guide
peaks.C File Reference
Tutorials » Spectrum tutorials

Detailed Description

View in nbviewer Open in SWAN Illustrates how to find peaks in histograms.

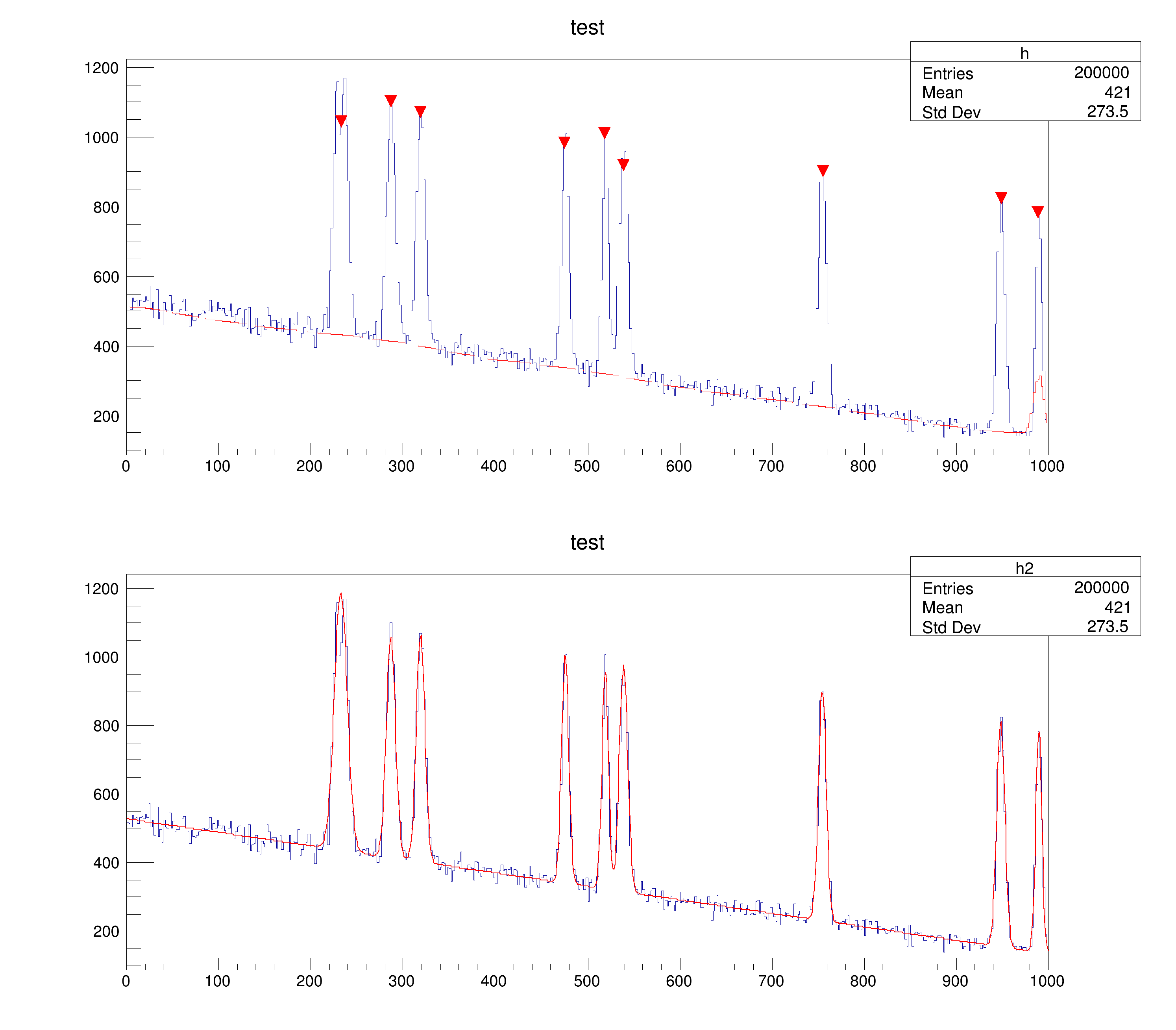
This script generates a random number of gaussian peaks on top of a linear background. The position of the peaks is found via TSpectrum and injected as initial values of parameters to make a global fit. The background is computed and drawn on top of the original histogram.

This script can fit "peaks' heights" or "peaks' areas" (comment out or uncomment the line which defines __PEAKS_C_FIT_AREAS__).

To execute this example, do (in ROOT 5 or ROOT 6):

root > .x peaks.C (generate 10 peaks by default)
root > .x peaks.C++ (use the compiler)
root > .x peaks.C++(30) (generates 30 peaks)
x
Double_t x[n]
Definition: legend1.C:17

To execute only the first part of the script (without fitting) specify a negative value for the number of peaks, eg

root > .x peaks.C(-20)
Found 9 candidate peaks to fit
Found 9 useful peaks to fit
Now fitting: Be patient
FCN=596.686 FROM MIGRAD STATUS=CONVERGED 1343 CALLS 1344 TOTAL
EDM=3.92392e-07 STRATEGY= 1 ERROR MATRIX UNCERTAINTY 4.1 per cent
EXT PARAMETER STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 p0 5.27684e+02 2.01895e+00 1.61337e-04 1.75611e-05
2 p1 -3.95030e-01 3.04733e-03 -2.24976e-07 9.00273e-03
3 p2 6.34691e+02 2.03922e+01 6.11343e-03 8.34700e-06
4 p3 5.19331e+02 9.71873e-02 -3.36434e-05 5.32034e-03
5 p4 3.49850e+00 1.08256e-01 -2.36209e-05 1.49297e-03
6 p5 6.64734e+02 1.64194e+01 -1.21344e-03 3.63148e-06
7 p6 3.19147e+02 1.05478e-01 7.08426e-06 2.00939e-04
8 p7 4.69148e+00 9.07160e-02 1.69389e-06 -1.62399e-03
9 p8 6.70930e+02 1.64206e+01 3.50063e-03 -9.49091e-06
10 p9 7.54806e+02 9.99565e-02 1.99123e-05 -2.47890e-03
11 p10 4.29726e+00 7.99677e-02 -3.50356e-05 -3.01094e-03
12 p11 6.69618e+02 1.73089e+01 -7.16995e-03 1.61496e-05
13 p12 4.75964e+02 9.46541e-02 -1.85498e-05 -6.93464e-04
14 p13 3.89327e+00 8.40808e-02 2.51847e-05 -4.75462e-03
15 p14 6.48094e+02 1.48388e+01 1.51648e-02 1.40873e-05
16 p15 9.89666e+02 7.93960e-02 2.05426e-08 5.80091e-03
17 p16 3.34529e+00 5.62112e-02 6.45922e-06 6.69573e-03
18 p17 6.62565e+02 1.83711e+01 9.37344e-03 1.71791e-05
19 p18 5.39268e+02 1.17175e-01 -4.07242e-05 2.90506e-04
20 p19 4.56057e+00 9.79810e-02 -3.17654e-05 1.67849e-03
21 p20 6.59405e+02 1.56865e+01 -5.02844e-03 1.33136e-05
22 p21 9.48476e+02 1.01997e-01 -2.38534e-05 -2.87561e-03
23 p22 4.41169e+00 8.80653e-02 3.30904e-05 -1.55483e-04
24 p23 7.53519e+02 1.46208e+01 -1.21918e-03 -1.58005e-05
25 p24 2.32585e+02 1.49583e-01 4.30086e-05 2.06782e-03
26 p25 6.95026e+00 1.18485e-01 1.79213e-05 3.79338e-04
27 p26 6.45490e+02 1.58541e+01 5.23845e-03 8.39699e-06
28 p27 2.86948e+02 1.20789e-01 7.08536e-05 -1.98488e-04
29 p28 4.98698e+00 9.92605e-02 -3.61574e-05 3.47101e-03
#include "TCanvas.h"
#include "TMath.h"
#include "TH1.h"
#include "TF1.h"
#include "TRandom.h"
#include "TSpectrum.h"
#include "TVirtualFitter.h"
//
// Comment out the line below, if you want "peaks' heights".
// Uncomment the line below, if you want "peaks' areas".
//
// #define __PEAKS_C_FIT_AREAS__ 1 /* fit peaks' areas */
Int_t npeaks = 30;
Double_t fpeaks(Double_t *x, Double_t *par) {
Double_t result = par[0] + par[1]*x[0];
for (Int_t p=0;p<npeaks;p++) {
Double_t norm = par[3*p+2]; // "height" or "area"
Double_t mean = par[3*p+3];
Double_t sigma = par[3*p+4];
#if defined(__PEAKS_C_FIT_AREAS__)
norm /= sigma * (TMath::Sqrt(TMath::TwoPi())); // "area"
#endif /* defined(__PEAKS_C_FIT_AREAS__) */
result += norm*TMath::Gaus(x[0],mean,sigma);
}
return result;
}
void peaks(Int_t np=10) {
npeaks = TMath::Abs(np);
TH1F *h = new TH1F("h","test",500,0,1000);
// Generate n peaks at random
Double_t par[3000];
par[0] = 0.8;
par[1] = -0.6/1000;
Int_t p;
for (p=0;p<npeaks;p++) {
par[3*p+2] = 1; // "height"
par[3*p+3] = 10+gRandom->Rndm()*980; // "mean"
par[3*p+4] = 3+2*gRandom->Rndm(); // "sigma"
#if defined(__PEAKS_C_FIT_AREAS__)
par[3*p+2] *= par[3*p+4] * (TMath::Sqrt(TMath::TwoPi())); // "area"
#endif /* defined(__PEAKS_C_FIT_AREAS__) */
}
TF1 *f = new TF1("f",fpeaks,0,1000,2+3*npeaks);
f->SetNpx(1000);
f->SetParameters(par);
TCanvas *c1 = new TCanvas("c1","c1",10,10,1000,900);
c1->Divide(1,2);
c1->cd(1);
h->FillRandom("f",200000);
h->Draw();
TH1F *h2 = (TH1F*)h->Clone("h2");
// Use TSpectrum to find the peak candidates
TSpectrum *s = new TSpectrum(2*npeaks);
Int_t nfound = s->Search(h,2,"",0.10);
printf("Found %d candidate peaks to fit\n",nfound);
// Estimate background using TSpectrum::Background
TH1 *hb = s->Background(h,20,"same");
if (hb) c1->Update();
if (np <0) return;
//estimate linear background using a fitting method
c1->cd(2);
TF1 *fline = new TF1("fline","pol1",0,1000);
h->Fit("fline","qn");
// Loop on all found peaks. Eliminate peaks at the background level
par[0] = fline->GetParameter(0);
par[1] = fline->GetParameter(1);
npeaks = 0;
Double_t *xpeaks;
xpeaks = s->GetPositionX();
for (p=0;p<nfound;p++) {
Double_t xp = xpeaks[p];
Int_t bin = h->GetXaxis()->FindBin(xp);
Double_t yp = h->GetBinContent(bin);
if (yp-TMath::Sqrt(yp) < fline->Eval(xp)) continue;
par[3*npeaks+2] = yp; // "height"
par[3*npeaks+3] = xp; // "mean"
par[3*npeaks+4] = 3; // "sigma"
#if defined(__PEAKS_C_FIT_AREAS__)
par[3*npeaks+2] *= par[3*npeaks+4] * (TMath::Sqrt(TMath::TwoPi())); // "area"
#endif /* defined(__PEAKS_C_FIT_AREAS__) */
npeaks++;
}
printf("Found %d useful peaks to fit\n",npeaks);
printf("Now fitting: Be patient\n");
TF1 *fit = new TF1("fit",fpeaks,0,1000,2+3*npeaks);
// We may have more than the default 25 parameters
TVirtualFitter::Fitter(h2,10+3*npeaks);
fit->SetParameters(par);
fit->SetNpx(1000);
h2->Fit("fit");
}
f
#define f(i)
Definition: RSha256.hxx:104
h
#define h(i)
Definition: RSha256.hxx:106
Int_t
int Int_t
Definition: RtypesCore.h:41
Double_t
double Double_t
Definition: RtypesCore.h:55
gRandom
R__EXTERN TRandom * gRandom
Definition: TRandom.h:62
TCanvas
The Canvas class.
Definition: TCanvas.h:31
TF1
1-Dim function class
Definition: TF1.h:211
TF1::SetNpx
virtual void SetNpx(Int_t npx=100)
Set the number of points used to draw the function.
Definition: TF1.cxx:3426
TF1::SetParameters
virtual void SetParameters(const Double_t *params)
Definition: TF1.h:628
TF1::Eval
virtual Double_t Eval(Double_t x, Double_t y=0, Double_t z=0, Double_t t=0) const
Evaluate this function.
Definition: TF1.cxx:1424
TF1::GetParameter
virtual Double_t GetParameter(Int_t ipar) const
Definition: TF1.h:496
TH1F
1-D histogram with a float per channel (see TH1 documentation)}
Definition: TH1.h:571
TH1
The TH1 histogram class.
Definition: TH1.h:56
TH1::Fit
virtual TFitResultPtr Fit(const char *formula, Option_t *option="", Option_t *goption="", Double_t xmin=0, Double_t xmax=0)
Fit histogram with function fname.
Definition: TH1.cxx:3695
TRandom::Rndm
virtual Double_t Rndm()
Machine independent random number generator.
Definition: TRandom.cxx:533
TSpectrum
Advanced Spectra Processing.
Definition: TSpectrum.h:18
TVirtualFitter::Fitter
static TVirtualFitter * Fitter(TObject *obj, Int_t maxpar=25)
Static function returning a pointer to the current fitter.
Definition: TVirtualFitter.cxx:159
sigma
const Double_t sigma
Definition: h1analysisProxy.h:11
c1
return c1
Definition: legend1.C:41
TGeoUnit::s
static constexpr double s
Definition: TGeoSystemOfUnits.h:162
TMath::Gaus
Double_t Gaus(Double_t x, Double_t mean=0, Double_t sigma=1, Bool_t norm=kFALSE)
Calculate a gaussian function with mean and sigma.
Definition: TMath.cxx:448
TMath::Sqrt
Double_t Sqrt(Double_t x)
Definition: TMath.h:679
TMath::Abs
Short_t Abs(Short_t d)
Definition: TMathBase.h:120
TMath::TwoPi
constexpr Double_t TwoPi()
Definition: TMath.h:45
Author
Rene Brun

Definition in file peaks.C.