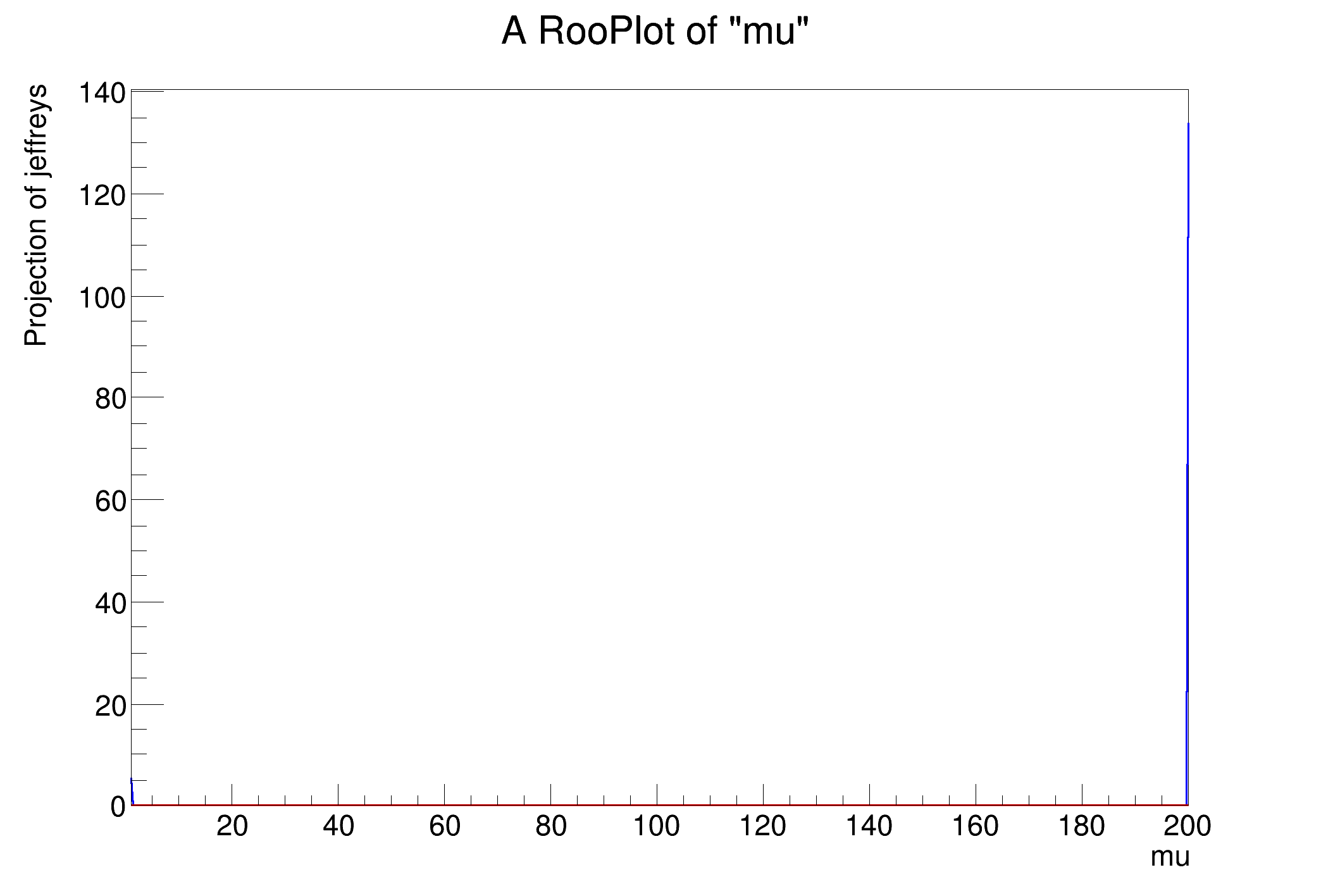
Jeffreys's prior is an 'objective prior' based on formal rules. It is calculated from the Fisher information matrix.
The analytic form is not known for most PDFs, but it is for simple cases like the Poisson mean, Gaussian mean, Gaussian sigma.
This class uses numerical tricks to calculate the Fisher Information Matrix efficiently. In particular, it takes advantage of a property of the 'Asimov data' as described in Asymptotic formulae for likelihood-based tests of new physics Glen Cowan, Kyle Cranmer, Eilam Gross, Ofer Vitells http://arxiv.org/abs/arXiv:1007.1727
␛[1mRooFit v3.60 -- Developed by Wouter Verkerke and David Kirkby␛[0m
Copyright (C) 2000-2013 NIKHEF, University of California & Stanford University
All rights reserved, please read http://roofit.sourceforge.net/license.txt
[#1] INFO:Minization -- p.d.f. provides expected number of events, including extended term in likelihood.
[#1] INFO:Minization -- createNLL: caching constraint set under name CONSTR_OF_PDF_p_FOR_OBS_x with 0 entries
[#1] INFO:Minization -- RooMinimizer::optimizeConst: activating const optimization
[#1] INFO:Minization -- The following expressions have been identified as constant and will be precalculated and cached: (u)
**********
** 1 **SET PRINT 1
**********
**********
** 2 **SET NOGRAD
**********
PARAMETER DEFINITIONS:
NO. NAME VALUE STEP SIZE LIMITS
1 mu 1.00000e+02 1.99000e+01 1.00000e+00 2.00000e+02
**********
** 3 **SET ERR 0.5
**********
**********
** 4 **SET PRINT 1
**********
**********
** 5 **SET STR 1
**********
NOW USING STRATEGY 1: TRY TO BALANCE SPEED AGAINST RELIABILITY
**********
** 6 **MIGRAD 500 1
**********
FIRST CALL TO USER FUNCTION AT NEW START POINT, WITH IFLAG=4.
START MIGRAD MINIMIZATION. STRATEGY 1. CONVERGENCE WHEN EDM .LT. 1.00e-03
FCN=-360.517 FROM MIGRAD STATUS=INITIATE 4 CALLS 5 TOTAL
EDM= unknown STRATEGY= 1 NO ERROR MATRIX
EXT PARAMETER CURRENT GUESS STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 mu 1.00000e+02 1.99000e+01 2.01361e-01 -5.66619e-05
ERR DEF= 0.5
MIGRAD MINIMIZATION HAS CONVERGED.
MIGRAD WILL VERIFY CONVERGENCE AND ERROR MATRIX.
COVARIANCE MATRIX CALCULATED SUCCESSFULLY
FCN=-360.517 FROM MIGRAD STATUS=CONVERGED 24 CALLS 25 TOTAL
EDM=4.72209e-14 STRATEGY= 1 ERROR MATRIX ACCURATE
EXT PARAMETER STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 mu 1.00000e+02 9.98317e+00 1.31866e-03 -2.16215e-06
ERR DEF= 0.5
EXTERNAL ERROR MATRIX. NDIM= 25 NPAR= 1 ERR DEF=0.5
1.000e+02
**********
** 7 **SET ERR 0.5
**********
**********
** 8 **SET PRINT 1
**********
**********
** 9 **HESSE 500
**********
COVARIANCE MATRIX CALCULATED SUCCESSFULLY
FCN=-360.517 FROM HESSE STATUS=OK 7 CALLS 32 TOTAL
EDM=9.50228e-17 STRATEGY= 1 ERROR MATRIX ACCURATE
EXT PARAMETER INTERNAL INTERNAL
NO. NAME VALUE ERROR STEP SIZE VALUE
1 mu 1.00000e+02 9.98317e+00 2.63731e-04 -5.02515e-03
ERR DEF= 0.5
EXTERNAL ERROR MATRIX. NDIM= 25 NPAR= 1 ERR DEF=0.5
1.000e+02
[#1] INFO:Fitting -- RooAbsPdf::fitTo(p) Calculating sum-of-weights-squared correction matrix for covariance matrix
**********
** 10 **SET ERR 0.5
**********
**********
** 11 **SET PRINT 1
**********
**********
** 12 **HESSE 500
**********
COVARIANCE MATRIX CALCULATED SUCCESSFULLY
FCN=-360.517 FROM HESSE STATUS=OK 5 CALLS 37 TOTAL
EDM=8.98159e-17 STRATEGY= 1 ERROR MATRIX ACCURATE
EXT PARAMETER INTERNAL INTERNAL
NO. NAME VALUE ERROR STEP SIZE VALUE
1 mu 1.00000e+02 9.98311e+00 1.05492e-05 -5.02515e-03
ERR DEF= 0.5
EXTERNAL ERROR MATRIX. NDIM= 25 NPAR= 1 ERR DEF=0.5
1.000e+02
[#1] INFO:Minization -- RooMinimizer::optimizeConst: deactivating const optimization
RooDataHist::genData[x] = 100 bins (100 weights)
RooFitResult: minimized FCN value: -360.517, estimated distance to minimum: 8.98159e-17
covariance matrix quality: Unknown, matrix was externally provided
Status : MINIMIZE=0 HESSE=0 HESSE=0
Floating Parameter FinalValue +/- Error
-------------------- --------------------------
mu 1.0000e+02 +/- 1.00e+01
variance = 100.001
stdev = 10.0001
jeffreys = 0.0999994
[#1] INFO:NumericIntegration -- RooRealIntegral::init(jeffreys_Int[mu]) using numeric integrator RooAdaptiveGaussKronrodIntegrator1D to calculate Int(mu)
[#0] ERROR:Integration -- RooAdaptiveGaussKronrodIntegrator1D::integral() ERROR: maximum number of subdivisions reached
[#1] INFO:NumericIntegration -- RooRealIntegral::init(test_Int[mu]) using numeric integrator RooIntegrator1D to calculate Int(mu)
void JeffreysPriorDemo(){
w.factory("Uniform::u(x[0,1])");
w.factory("mu[100,1,200]");
w.factory("ExtendPdf::p(u,mu)");
w.defineSet("poi","mu");
w.defineSet("obs","x");
RooPlot* plot = w.var(
"mu")->frame();
}
void TestJeffreysGaussMean(){
w.factory("Gaussian::g(x[0,-20,20],mu[0,-5,5],sigma[1,0,10])");
w.factory("n[10,.1,200]");
w.factory("ExtendPdf::p(g,n)");
w.var("sigma")->setConstant();
w.var("n")->setConstant();
w.defineSet("poi","mu");
w.defineSet("obs","x");
pi.getParameters(*temp)->Print();
RooPlot* plot = w.var(
"mu")->frame();
}
void TestJeffreysGaussSigma(){
w.factory("Gaussian::g(x[0,-20,20],mu[0,-5,5],sigma[1,1,5])");
w.factory("n[100,.1,2000]");
w.factory("ExtendPdf::p(g,n)");
w.var("mu")->setConstant();
w.var("n")->setConstant();
w.var("x")->setBins(301);
w.defineSet("poi","sigma");
w.defineSet("obs","x");
pi.specialIntegratorConfig(
kTRUE)->getConfigSection(
"RooIntegrator1D").setRealValue(
"maxSteps",3);
pi.getParameters(*temp)->Print();
RooPlot* plot = w.var(
"sigma")->frame();
}
void TestJeffreysGaussMeanAndSigma(){
w.factory("Gaussian::g(x[0,-20,20],mu[0,-5,5],sigma[1,1,5])");
w.factory("n[100,.1,2000]");
w.factory("ExtendPdf::p(g,n)");
w.var("n")->setConstant();
w.var("x")->setBins(301);
w.defineSet("poi","mu,sigma");
w.defineSet("obs","x");
pi.specialIntegratorConfig(
kTRUE)->getConfigSection(
"RooIntegrator1D").setRealValue(
"maxSteps",3);
pi.getParameters(*temp)->Print();
}
virtual void Print(Option_t *options=0) const
Print TNamed name and title.
RooArgSet is a container object that can hold multiple RooAbsArg objects.
RooDataSet is a container class to hold N-dimensional binned data.
RooFitResult is a container class to hold the input and output of a PDF fit to a dataset.
virtual void Print(Option_t *options=0) const
Print TNamed name and title.
const TMatrixDSym & covarianceMatrix() const
Return covariance matrix.
RooGenericPdf is a concrete implementation of a probability density function, which takes a RooArgLis...
A RooPlot is a plot frame and a container for graphics objects within that frame.
virtual void Draw(Option_t *options=0)
Draw this plot and all of the elements it contains.
The RooWorkspace is a persistable container for RooFit projects.
virtual void Draw(Option_t *option="")
Draw this histogram with options.
virtual Double_t Determinant() const
TMatrixTSym< Element > & Invert(Double_t *det=0)
Invert the matrix and calculate its determinant Notice that the LU decomposition is used instead of B...
RooCmdArg Binning(const RooAbsBinning &binning)
RooCmdArg YVar(const RooAbsRealLValue &var, const RooCmdArg &arg=RooCmdArg::none())
RooCmdArg SumW2Error(Bool_t flag)
RooCmdArg Save(Bool_t flag=kTRUE)
RooCmdArg ExpectedData(Bool_t flag=kTRUE)
RooCmdArg LineColor(Color_t color)
RooCmdArg LineStyle(Style_t style)
static constexpr double pi



 tutorial demonstrating and validates the RooJeffreysPrior class
tutorial demonstrating and validates the RooJeffreysPrior class