HybridOriginalDemo.C File Reference

Detailed Description

Example on how to use the HybridCalculatorOriginal class

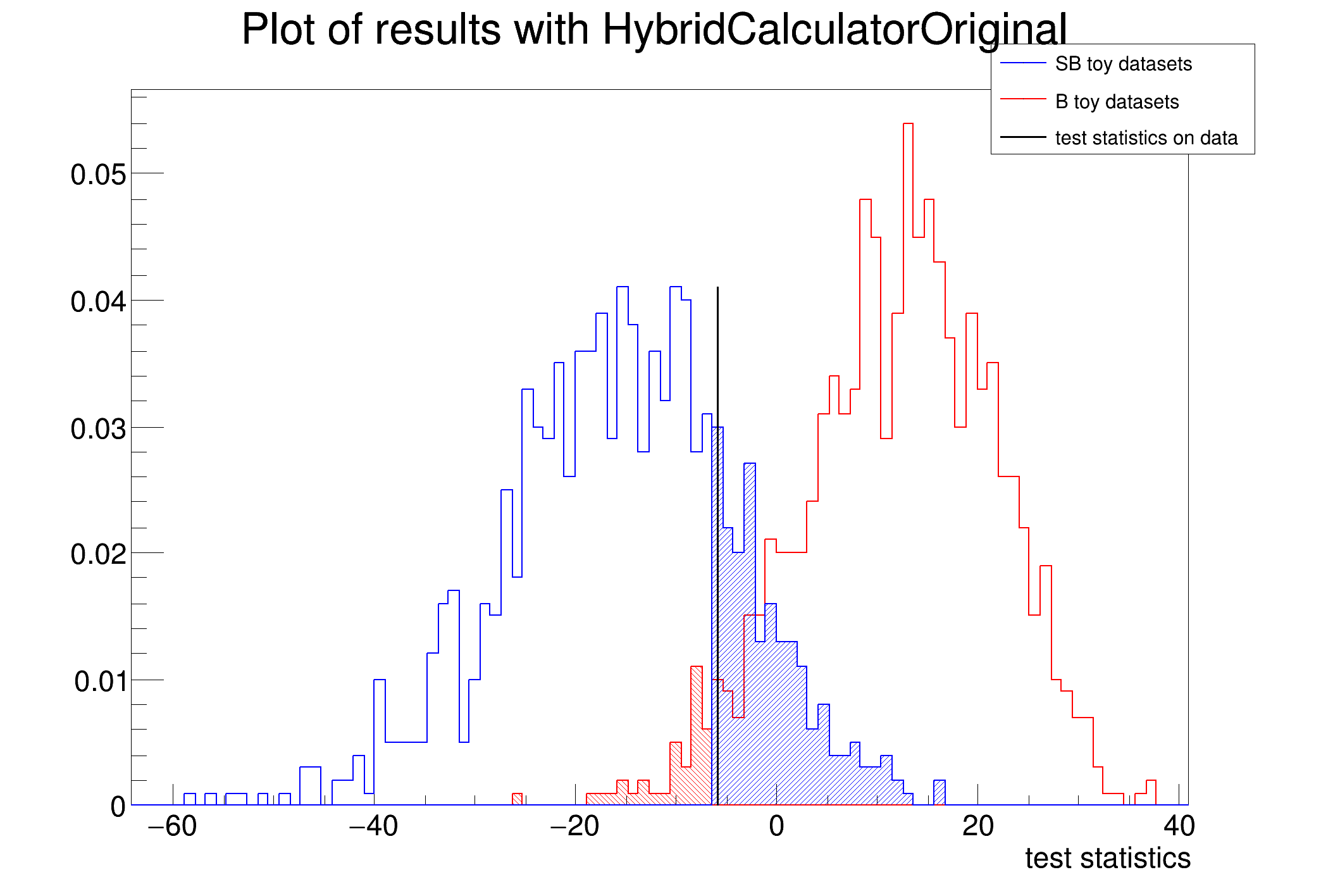
With this example, you should get: CL_sb = 0.130 and CL_b = 0.946 (if data had -2lnQ = -3.0742).

 
 
␛[1mRooFit v3.60 -- Developed by Wouter Verkerke and David Kirkby␛[0m 
                Copyright (C) 2000-2013 NIKHEF, University of California & Stanford University
                All rights reserved, please read http://roofit.sourceforge.net/license.txt
 
Test statistics has been evaluated for data
HybridCalculatorOriginal: run 1000 toy-MC experiments
with test statistics index: 1
marginalize nuisance parameters 
....... toy number 0 / 1000
....... toy number 500 / 1000
Completed HybridCalculatorOriginal example:
 - -2lnQ = -5.97789
 - CL_sb = 0.194
 - CL_b  = 0.04
 - CL_s  = 4.85
 - significance of data  = 1.75069
 - mean significance of toys  = 2.65207

 
#include "RooRandom.h"
#include "RooRealVar.h"
#include "RooGaussian.h"
#include "RooPolynomial.h"
#include "RooArgSet.h"
#include "RooAddPdf.h"
#include "RooDataSet.h"
#include "RooExtendPdf.h"
#include "RooConstVar.h"
#include "RooStats/HybridCalculatorOriginal.h"
#include "RooStats/HybridResult.h"
#include "RooStats/HybridPlot.h"
 
void HybridOriginalDemo(int ntoys = 1000)
{
   using namespace RooFit;
   using namespace RooStats;
 
   // set RooFit random seed
   RooRandom::randomGenerator()->SetSeed(3007);
 
   /// build the models for background and signal+background
   RooRealVar x("x","",-3,3);
   RooArgList observables(x); // variables to be generated
 
   // gaussian signal
   RooGaussian sig_pdf("sig_pdf","",x, RooConst(0.0),RooConst(0.8));
   RooRealVar sig_yield("sig_yield","",20,0,300);
 
   // flat background (extended PDF)
   RooPolynomial bkg_pdf("bkg_pdf","", x, RooConst(0));
   RooRealVar bkg_yield("bkg_yield","",40,0,300);
   RooExtendPdf bkg_ext_pdf("bkg_ext_pdf","",bkg_pdf,bkg_yield);
 
   //  bkg_yield.setConstant(kTRUE);
   sig_yield.setConstant(kTRUE);
 
   // total sig+bkg (extended PDF)
   RooAddPdf tot_pdf("tot_pdf","",RooArgList(sig_pdf,bkg_pdf),RooArgList(sig_yield,bkg_yield));
 
   // build the prior PDF on the parameters to be integrated
   // gaussian contraint on the background yield ( N_B = 40 +/- 10  ie. 25% )
   RooGaussian bkg_yield_prior("bkg_yield_prior","",bkg_yield,RooConst(bkg_yield.getVal()),RooConst(10.));
 
   RooArgSet nuisance_parameters(bkg_yield); // variables to be integrated
 
   /// generate a data sample
   RooDataSet* data = tot_pdf.generate(observables,RooFit::Extended());
 
   // run HybridCalculator on those inputs
   // use interface from HypoTest calculator by default
 
   HybridCalculatorOriginal myHybridCalc(*data, tot_pdf , bkg_ext_pdf ,
                                   &nuisance_parameters, &bkg_yield_prior);
 
   // here I use the default test statistics: 2*lnQ (optional)
   myHybridCalc.SetTestStatistic(1);
   //myHybridCalc.SetTestStatistic(3); // profile likelihood ratio
 
   myHybridCalc.SetNumberOfToys(ntoys);
   myHybridCalc.UseNuisance(true);
 
   // for speed up generation (do binned data)
   myHybridCalc.SetGenerateBinned(false);
 
   // calculate by running ntoys for the S+B and B hypothesis and retrieve the result
   HybridResult* myHybridResult = myHybridCalc.GetHypoTest();
 
   if (! myHybridResult) {
     std::cerr << "\nError returned from Hypothesis test" << std::endl;
     return;
   }
 
   /// nice plot of the results
   HybridPlot* myHybridPlot = myHybridResult->GetPlot("myHybridPlot","Plot of results with HybridCalculatorOriginal",100);
   myHybridPlot->Draw();
 
   /// recover and display the results
   double clsb_data = myHybridResult->CLsplusb();
   double clb_data = myHybridResult->CLb();
   double cls_data = myHybridResult->CLs();
   double data_significance = myHybridResult->Significance();
   double min2lnQ_data = myHybridResult->GetTestStat_data();
 
   /// compute the mean expected significance from toys
   double mean_sb_toys_test_stat = myHybridPlot->GetSBmean();
   myHybridResult->SetDataTestStatistics(mean_sb_toys_test_stat);
   double toys_significance = myHybridResult->Significance();
 
   std::cout << "Completed HybridCalculatorOriginal example:\n";
   std::cout << " - -2lnQ = " << min2lnQ_data << endl;
   std::cout << " - CL_sb = " << clsb_data << std::endl;
   std::cout << " - CL_b  = " << clb_data << std::endl;
   std::cout << " - CL_s  = " << cls_data << std::endl;
   std::cout << " - significance of data  = " << data_significance << std::endl;
   std::cout << " - mean significance of toys  = " << toys_significance << std::endl;
}
 
 

Author

Gregory Schott

Definition in file HybridOriginalDemo.C.