Logo ROOT   6.14/05
Reference Guide
rf609_xychi2fit.C File Reference
Tutorials » RooFit Tutorials

Detailed Description

View in nbviewer Open in SWAN 'LIKELIHOOD AND MINIMIZATION' RooFit tutorial macro #609

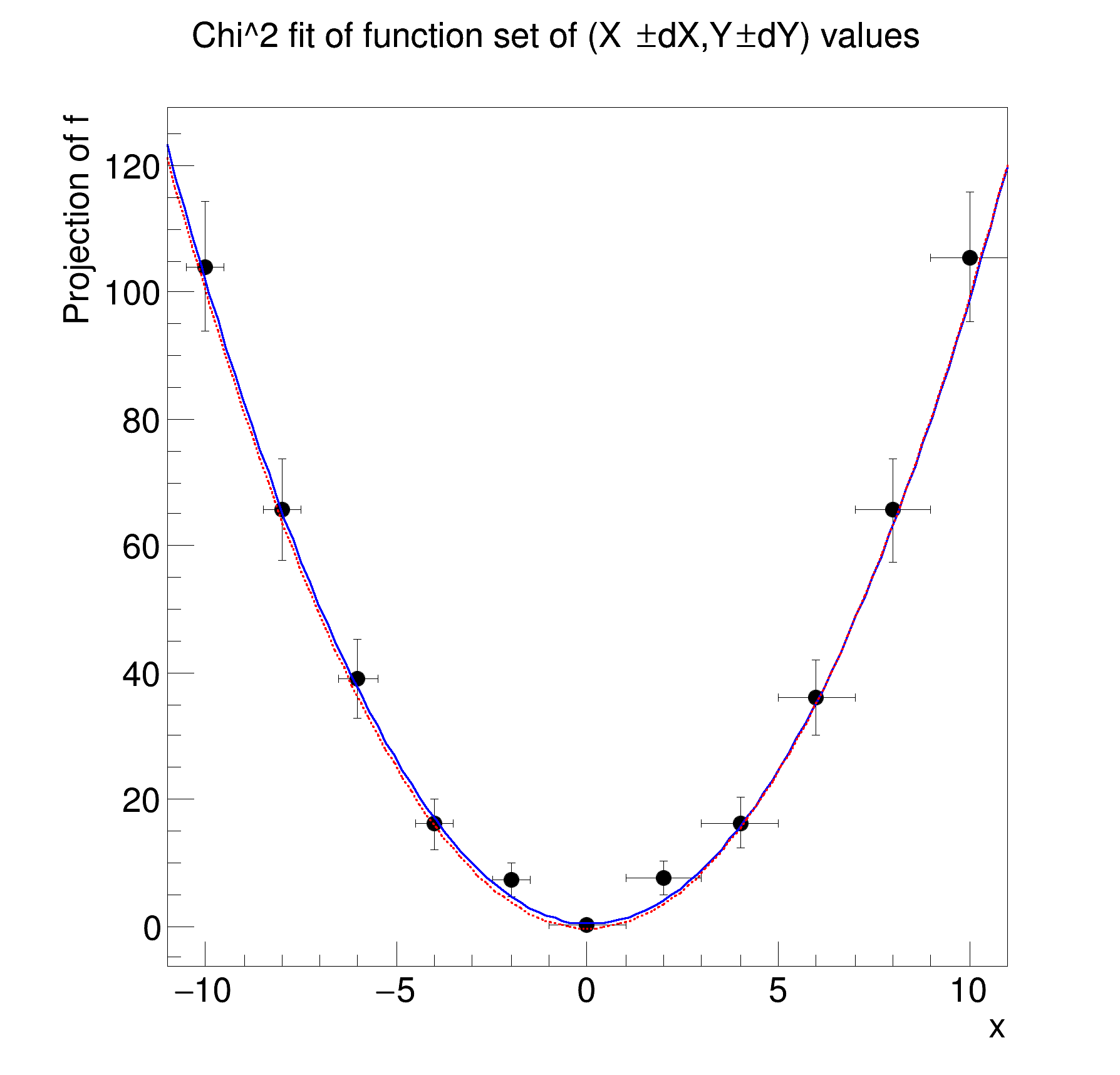
Setting up a chi^2 fit to an unbinned dataset with X,Y,err(Y) values (and optionally err(X) values)

pict1_rf609_xychi2fit.C.png
Processing /mnt/build/workspace/root-makedoc-v614/rootspi/rdoc/src/v6-14-00-patches/tutorials/roofit/rf609_xychi2fit.C...
RooFit v3.60 -- Developed by Wouter Verkerke and David Kirkby
Copyright (C) 2000-2013 NIKHEF, University of California & Stanford University
All rights reserved, please read http://roofit.sourceforge.net/license.txt
[#1] INFO:Minization -- RooMinimizer::optimizeConst: activating const optimization
**********
** 1 **SET PRINT 1
**********
**********
** 2 **SET NOGRAD
**********
PARAMETER DEFINITIONS:
NO. NAME VALUE STEP SIZE LIMITS
1 a 0.00000e+00 2.00000e+00 -1.00000e+01 1.00000e+01
2 b 0.00000e+00 2.00000e+01 -1.00000e+02 1.00000e+02
**********
** 3 **SET ERR 1
**********
**********
** 4 **SET PRINT 1
**********
**********
** 5 **SET STR 1
**********
NOW USING STRATEGY 1: TRY TO BALANCE SPEED AGAINST RELIABILITY
**********
** 6 **MIGRAD 1000 1
**********
FIRST CALL TO USER FUNCTION AT NEW START POINT, WITH IFLAG=4.
START MIGRAD MINIMIZATION. STRATEGY 1. CONVERGENCE WHEN EDM .LT. 1.00e-03
FCN=2.04222 FROM MIGRAD STATUS=INITIATE 8 CALLS 9 TOTAL
EDM= unknown STRATEGY= 1 NO ERROR MATRIX
EXT PARAMETER CURRENT GUESS STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 a 0.00000e+00 2.00000e+00 2.01358e-01 1.35235e+01
2 b 0.00000e+00 2.00000e+01 2.01358e-01 -3.08578e+02
MIGRAD MINIMIZATION HAS CONVERGED.
MIGRAD WILL VERIFY CONVERGENCE AND ERROR MATRIX.
COVARIANCE MATRIX CALCULATED SUCCESSFULLY
FCN=1.43197 FROM MIGRAD STATUS=CONVERGED 32 CALLS 33 TOTAL
EDM=3.23329e-05 STRATEGY= 1 ERROR MATRIX ACCURATE
EXT PARAMETER STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 a -1.60654e-01 5.24023e-01 3.93124e-05 1.09375e-01
2 b 3.34226e-01 4.91235e-01 3.85614e-06 -1.06196e+00
EXTERNAL ERROR MATRIX. NDIM= 25 NPAR= 2 ERR DEF=1
2.749e-01 -1.964e-02
-1.964e-02 2.413e-01
PARAMETER CORRELATION COEFFICIENTS
NO. GLOBAL 1 2
1 0.07625 1.000 -0.076
2 0.07625 -0.076 1.000
**********
** 7 **SET ERR 1
**********
**********
** 8 **SET PRINT 1
**********
**********
** 9 **HESSE 1000
**********
COVARIANCE MATRIX CALCULATED SUCCESSFULLY
FCN=1.43197 FROM HESSE STATUS=OK 10 CALLS 43 TOTAL
EDM=3.23291e-05 STRATEGY= 1 ERROR MATRIX ACCURATE
EXT PARAMETER INTERNAL INTERNAL
NO. NAME VALUE ERROR STEP SIZE VALUE
1 a -1.60654e-01 5.24019e-01 7.86248e-06 -1.60660e-02
2 b 3.34226e-01 4.91231e-01 7.71228e-07 3.34226e-03
EXTERNAL ERROR MATRIX. NDIM= 25 NPAR= 2 ERR DEF=1
2.748e-01 -1.961e-02
-1.961e-02 2.413e-01
PARAMETER CORRELATION COEFFICIENTS
NO. GLOBAL 1 2
1 0.07614 1.000 -0.076
2 0.07614 -0.076 1.000
[#1] INFO:Minization -- RooMinimizer::optimizeConst: activating const optimization
**********
** 10 **SET PRINT 1
**********
**********
** 11 **SET NOGRAD
**********
PARAMETER DEFINITIONS:
NO. NAME VALUE STEP SIZE LIMITS
1 a -1.60654e-01 5.24019e-01 -1.00000e+01 1.00000e+01
2 b 3.34226e-01 4.91231e-01 -1.00000e+02 1.00000e+02
**********
** 12 **SET ERR 1
**********
**********
** 13 **SET PRINT 1
**********
**********
** 14 **SET STR 1
**********
NOW USING STRATEGY 1: TRY TO BALANCE SPEED AGAINST RELIABILITY
**********
** 15 **MIGRAD 1000 1
**********
FIRST CALL TO USER FUNCTION AT NEW START POINT, WITH IFLAG=4.
START MIGRAD MINIMIZATION. STRATEGY 1. CONVERGENCE WHEN EDM .LT. 1.00e-03
FCN=176984 FROM MIGRAD STATUS=INITIATE 8 CALLS 9 TOTAL
EDM= unknown STRATEGY= 1 NO ERROR MATRIX
EXT PARAMETER CURRENT GUESS STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 a -1.60654e-01 5.24019e-01 5.24327e-02 -8.81282e+03
2 b 3.34226e-01 4.91231e-01 4.91235e-03 2.93731e+07
MIGRAD MINIMIZATION HAS CONVERGED.
MIGRAD WILL VERIFY CONVERGENCE AND ERROR MATRIX.
COVARIANCE MATRIX CALCULATED SUCCESSFULLY
FCN=76478.7 FROM MIGRAD STATUS=CONVERGED 30 CALLS 31 TOTAL
EDM=2.56889e-08 STRATEGY= 1 ERROR MATRIX ACCURATE
EXT PARAMETER STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 a -5.61220e-02 1.57588e-02 2.12800e-04 -1.43819e-01
2 b -3.49788e-01 2.15812e-03 2.91421e-06 -1.32588e-01
EXTERNAL ERROR MATRIX. NDIM= 25 NPAR= 2 ERR DEF=1
2.483e-04 3.343e-08
3.343e-08 4.657e-06
PARAMETER CORRELATION COEFFICIENTS
NO. GLOBAL 1 2
1 0.00098 1.000 0.001
2 0.00098 0.001 1.000
**********
** 16 **SET ERR 1
**********
**********
** 17 **SET PRINT 1
**********
**********
** 18 **HESSE 1000
**********
COVARIANCE MATRIX CALCULATED SUCCESSFULLY
FCN=76478.7 FROM HESSE STATUS=OK 10 CALLS 41 TOTAL
EDM=2.56903e-08 STRATEGY= 1 ERROR MATRIX ACCURATE
EXT PARAMETER INTERNAL INTERNAL
NO. NAME VALUE ERROR STEP SIZE VALUE
1 a -5.61220e-02 1.57588e-02 4.25601e-05 -5.61223e-03
2 b -3.49788e-01 2.15812e-03 5.82843e-07 -3.49789e-03
EXTERNAL ERROR MATRIX. NDIM= 25 NPAR= 2 ERR DEF=1
2.483e-04 3.343e-08
3.343e-08 4.657e-06
PARAMETER CORRELATION COEFFICIENTS
NO. GLOBAL 1 2
1 0.00098 1.000 0.001
2 0.00098 0.001 1.000
#include "RooRealVar.h"
#include "RooDataSet.h"
#include "RooPolyVar.h"
#include "RooConstVar.h"
#include "RooChi2Var.h"
#include "TCanvas.h"
#include "TAxis.h"
#include "RooPlot.h"
#include "TRandom.h"
using namespace RooFit ;
void rf609_xychi2fit()
{
// C r e a t e d a t a s e t w i t h X a n d Y v a l u e s
// -------------------------------------------------------------------
// Make weighted XY dataset with asymmetric errors stored
// The StoreError() argument is essential as it makes
// the dataset store the error in addition to the values
// of the observables. If errors on one or more observables
// are asymmetric, one can store the asymmetric error
// using the StoreAsymError() argument
RooRealVar x("x","x",-11,11) ;
RooRealVar y("y","y",-10,200) ;
RooDataSet dxy("dxy","dxy",RooArgSet(x,y),StoreError(RooArgSet(x,y))) ;
// Fill an example dataset with X,err(X),Y,err(Y) values
for (int i=0 ; i<=10 ; i++) {
// Set X value and error
x = -10 + 2*i;
x.setError( i<5 ? 0.5/1. : 1.0/1. ) ;
// Set Y value and error
y = x.getVal() * x.getVal() + 4*fabs(gRandom->Gaus()) ;
y.setError(sqrt(y.getVal())) ;
dxy.add(RooArgSet(x,y)) ;
}
// P e r f o r m c h i 2 f i t t o X + / - d x a n d Y + / - d Y v a l u e s
// ---------------------------------------------------------------------------------------
// Make fit function
RooRealVar a("a","a",0.0,-10,10) ;
RooRealVar b("b","b",0.0,-100,100) ;
RooPolyVar f("f","f",x,RooArgList(b,a,RooConst(1))) ;
// Plot dataset in X-Y interpretation
RooPlot* frame = x.frame(Title("Chi^2 fit of function set of (X#pmdX,Y#pmdY) values")) ;
dxy.plotOnXY(frame,YVar(y)) ;
// Fit chi^2 using X and Y errors
f.chi2FitTo(dxy,YVar(y)) ;
// Overlay fitted function
f.plotOn(frame) ;
// Alternative: fit chi^2 integrating f(x) over ranges defined by X errors, rather
// than taking point at center of bin
f.chi2FitTo(dxy,YVar(y),Integrate(kTRUE)) ;
// Overlay alternate fit result
f.plotOn(frame,LineStyle(kDashed),LineColor(kRed)) ;
// Draw the plot on a canvas
new TCanvas("rf609_xychi2fit","rf609_xychi2fit",600,600) ;
gPad->SetLeftMargin(0.15) ; frame->GetYaxis()->SetTitleOffset(1.4) ; frame->Draw() ;
}
Author
07/2008 - Wouter Verkerke

Definition in file rf609_xychi2fit.C.