Logo ROOT   6.12/07
Reference Guide
rf403_weightedevts.C File Reference
Tutorials » RooFit Tutorials

Detailed Description

View in nbviewer Open in SWAN 'DATA AND CATEGORIES' RooFit tutorial macro #403

Using weights in unbinned datasets

pict1_rf403_weightedevts.C.png
Processing /mnt/build/workspace/root-makedoc-v612/rootspi/rdoc/src/v6-12-00-patches/tutorials/roofit/rf403_weightedevts.C...
RooFit v3.60 -- Developed by Wouter Verkerke and David Kirkby
Copyright (C) 2000-2013 NIKHEF, University of California & Stanford University
All rights reserved, please read http://roofit.sourceforge.net/license.txt
RooDataSet::pxData[x,w] = 1000 entries
RooDataSet::pxData[x,weight:w] = 1000 entries (43238.9 weighted)
[#0] WARNING:InputArguments -- RooAbsPdf::fitTo(p2) WARNING: a likelihood fit is request of what appears to be weighted data.
While the estimated values of the parameters will always be calculated taking the weights into account,
there are multiple ways to estimate the errors on these parameter values. You are advised to make an
explicit choice on the error calculation:
- Either provide SumW2Error(kTRUE), to calculate a sum-of-weights corrected HESSE error matrix
(error will be proportional to the number of events)
- Or provide SumW2Error(kFALSE), to return errors from original HESSE error matrix
(which will be proportional to the sum of the weights)
If you want the errors to reflect the information contained in the provided dataset, choose kTRUE.
If you want the errors to reflect the precision you would be able to obtain with an unweighted dataset
with 'sum-of-weights' events, choose kFALSE.
[#1] INFO:Minization -- RooMinimizer::optimizeConst: activating const optimization
[#0] WARNING:Optimization -- RooAbsOptTestStatistic::optimizeConstantTerms(nll_p2_pxData) WARNING Cache-and-track optimization (Optimize level 2) is only available for datasets implement in terms of RooVectorDataStore - ignoring this option for current dataset
**********
** 1 **SET PRINT 1
**********
**********
** 2 **SET NOGRAD
**********
PARAMETER DEFINITIONS:
NO. NAME VALUE STEP SIZE LIMITS
1 a1 0.00000e+00 2.00000e-01 -1.00000e+00 1.00000e+00
2 a2 1.00000e+00 5.00000e-01 0.00000e+00 1.00000e+01
**********
** 3 **SET ERR 0.5
**********
**********
** 4 **SET PRINT 1
**********
**********
** 5 **SET STR 1
**********
NOW USING STRATEGY 1: TRY TO BALANCE SPEED AGAINST RELIABILITY
**********
** 6 **MIGRAD 1000 1
**********
FIRST CALL TO USER FUNCTION AT NEW START POINT, WITH IFLAG=4.
START MIGRAD MINIMIZATION. STRATEGY 1. CONVERGENCE WHEN EDM .LT. 1.00e-03
FCN=119822 FROM MIGRAD STATUS=INITIATE 25 CALLS 26 TOTAL
EDM= unknown STRATEGY= 1 NO ERROR MATRIX
EXT PARAMETER CURRENT GUESS STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 a1 0.00000e+00 2.00000e-01 0.00000e+00 1.68737e+02
2 a2 1.52215e-01 5.00000e-01 -3.96120e-01 4.87454e+03
ERR DEF= 0.5
MIGRAD MINIMIZATION HAS CONVERGED.
MIGRAD WILL VERIFY CONVERGENCE AND ERROR MATRIX.
COVARIANCE MATRIX CALCULATED SUCCESSFULLY
FCN=119682 FROM MIGRAD STATUS=CONVERGED 63 CALLS 64 TOTAL
EDM=1.29222e-07 STRATEGY= 1 ERROR MATRIX ACCURATE
EXT PARAMETER STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 a1 -4.85603e-03 4.03455e-03 9.64266e-04 -8.28728e-02
2 a2 9.86514e-02 2.41306e-03 5.83664e-04 -5.42318e-02
ERR DEF= 0.5
EXTERNAL ERROR MATRIX. NDIM= 25 NPAR= 2 ERR DEF=0.5
1.628e-05 -1.173e-08
-1.173e-08 5.823e-06
PARAMETER CORRELATION COEFFICIENTS
NO. GLOBAL 1 2
1 0.00120 1.000 -0.001
2 0.00120 -0.001 1.000
**********
** 7 **SET ERR 0.5
**********
**********
** 8 **SET PRINT 1
**********
**********
** 9 **HESSE 1000
**********
COVARIANCE MATRIX CALCULATED SUCCESSFULLY
FCN=119682 FROM HESSE STATUS=OK 10 CALLS 74 TOTAL
EDM=1.28662e-07 STRATEGY= 1 ERROR MATRIX ACCURATE
EXT PARAMETER INTERNAL INTERNAL
NO. NAME VALUE ERROR STEP SIZE VALUE
1 a1 -4.85603e-03 4.03459e-03 1.92853e-04 -4.85605e-03
2 a2 9.86514e-02 2.41310e-03 2.33465e-05 -1.37182e+00
ERR DEF= 0.5
EXTERNAL ERROR MATRIX. NDIM= 25 NPAR= 2 ERR DEF=0.5
1.628e-05 -4.575e-08
-4.575e-08 5.823e-06
PARAMETER CORRELATION COEFFICIENTS
NO. GLOBAL 1 2
1 0.00470 1.000 -0.005
2 0.00470 -0.005 1.000
[#1] INFO:Minization -- RooMinimizer::optimizeConst: deactivating const optimization
[#1] INFO:Minization -- RooMinimizer::optimizeConst: activating const optimization
[#0] WARNING:Optimization -- RooAbsOptTestStatistic::optimizeConstantTerms(nll_p2_pxData) WARNING Cache-and-track optimization (Optimize level 2) is only available for datasets implement in terms of RooVectorDataStore - ignoring this option for current dataset
**********
** 10 **SET PRINT 1
**********
**********
** 11 **SET NOGRAD
**********
PARAMETER DEFINITIONS:
NO. NAME VALUE STEP SIZE LIMITS
1 a1 -4.85603e-03 4.03459e-03 -1.00000e+00 1.00000e+00
2 a2 9.86514e-02 2.41310e-03 0.00000e+00 1.00000e+01
**********
** 12 **SET ERR 0.5
**********
**********
** 13 **SET PRINT 1
**********
**********
** 14 **SET STR 1
**********
NOW USING STRATEGY 1: TRY TO BALANCE SPEED AGAINST RELIABILITY
**********
** 15 **MIGRAD 1000 1
**********
FIRST CALL TO USER FUNCTION AT NEW START POINT, WITH IFLAG=4.
START MIGRAD MINIMIZATION. STRATEGY 1. CONVERGENCE WHEN EDM .LT. 1.00e-03
FCN=119682 FROM MIGRAD STATUS=INITIATE 4 CALLS 5 TOTAL
EDM= unknown STRATEGY= 1 NO ERROR MATRIX
EXT PARAMETER CURRENT GUESS STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 a1 -4.85603e-03 4.03459e-03 4.03465e-03 -8.32948e-02
2 a2 9.86514e-02 2.41310e-03 2.44179e-03 -2.65748e-01
ERR DEF= 0.5
MIGRAD MINIMIZATION HAS CONVERGED.
MIGRAD WILL VERIFY CONVERGENCE AND ERROR MATRIX.
COVARIANCE MATRIX CALCULATED SUCCESSFULLY
FCN=119682 FROM MIGRAD STATUS=CONVERGED 23 CALLS 24 TOTAL
EDM=5.53437e-08 STRATEGY= 1 ERROR MATRIX ACCURATE
EXT PARAMETER STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 a1 -4.85553e-03 4.03456e-03 9.63830e-04 -5.18346e-02
2 a2 9.86520e-02 2.41308e-03 5.83268e-04 4.40227e-02
ERR DEF= 0.5
EXTERNAL ERROR MATRIX. NDIM= 25 NPAR= 2 ERR DEF=0.5
1.628e-05 -1.171e-08
-1.171e-08 5.823e-06
PARAMETER CORRELATION COEFFICIENTS
NO. GLOBAL 1 2
1 0.00120 1.000 -0.001
2 0.00120 -0.001 1.000
**********
** 16 **SET ERR 0.5
**********
**********
** 17 **SET PRINT 1
**********
**********
** 18 **HESSE 1000
**********
COVARIANCE MATRIX CALCULATED SUCCESSFULLY
FCN=119682 FROM HESSE STATUS=OK 10 CALLS 34 TOTAL
EDM=5.56466e-08 STRATEGY= 1 ERROR MATRIX ACCURATE
EXT PARAMETER INTERNAL INTERNAL
NO. NAME VALUE ERROR STEP SIZE VALUE
1 a1 -4.85553e-03 4.03461e-03 1.92766e-04 -4.85555e-03
2 a2 9.86520e-02 2.41312e-03 2.33307e-05 -1.37182e+00
ERR DEF= 0.5
EXTERNAL ERROR MATRIX. NDIM= 25 NPAR= 2 ERR DEF=0.5
1.628e-05 -4.571e-08
-4.571e-08 5.823e-06
PARAMETER CORRELATION COEFFICIENTS
NO. GLOBAL 1 2
1 0.00470 1.000 -0.005
2 0.00470 -0.005 1.000
[#1] INFO:Fitting -- RooAbsPdf::fitTo(p2) Calculating sum-of-weights-squared correction matrix for covariance matrix
**********
** 19 **SET ERR 0.5
**********
**********
** 20 **SET PRINT 1
**********
**********
** 21 **HESSE 1000
**********
COVARIANCE MATRIX CALCULATED SUCCESSFULLY
FCN=6.84247e+06 FROM HESSE STATUS=OK 14 CALLS 48 TOTAL
EDM=158914 STRATEGY= 1 ERROR MATRIX ACCURATE
EXT PARAMETER INTERNAL INTERNAL
NO. NAME VALUE ERROR STEP SIZE VALUE
1 a1 -4.85553e-03 5.43362e-04 3.93243e-03 -4.85555e-03
2 a2 9.86520e-02 1.95133e-04 4.75947e-04 -1.37182e+00
ERR DEF= 0.5
EXTERNAL ERROR MATRIX. NDIM= 25 NPAR= 2 ERR DEF=0.5
2.952e-07 6.228e-09
6.228e-09 3.808e-08
PARAMETER CORRELATION COEFFICIENTS
NO. GLOBAL 1 2
1 0.05874 1.000 0.059
2 0.05874 0.059 1.000
[#1] INFO:Minization -- RooMinimizer::optimizeConst: deactivating const optimization
[#1] INFO:NumericIntegration -- RooRealIntegral::init(genPdf_Int[x]) using numeric integrator RooIntegrator1D to calculate Int(x)
[#1] INFO:NumericIntegration -- RooRealIntegral::init(genPdf_Int[x]) using numeric integrator RooIntegrator1D to calculate Int(x)
[#1] INFO:NumericIntegration -- RooRealIntegral::init(genPdf_Int[x]) using numeric integrator RooIntegrator1D to calculate Int(x)
[#1] INFO:NumericIntegration -- RooRealIntegral::init(genPdf_Int[x]) using numeric integrator RooIntegrator1D to calculate Int(x)
[#1] INFO:Minization -- RooMinimizer::optimizeConst: activating const optimization
**********
** 22 **SET PRINT 1
**********
**********
** 23 **SET NOGRAD
**********
PARAMETER DEFINITIONS:
NO. NAME VALUE STEP SIZE LIMITS
1 a1 -4.85553e-03 3.00247e-02 -1.00000e+00 1.00000e+00
2 a2 9.86520e-02 2.98987e-02 0.00000e+00 1.00000e+01
**********
** 24 **SET ERR 0.5
**********
**********
** 25 **SET PRINT 1
**********
**********
** 26 **SET STR 1
**********
NOW USING STRATEGY 1: TRY TO BALANCE SPEED AGAINST RELIABILITY
**********
** 27 **MIGRAD 1000 1
**********
FIRST CALL TO USER FUNCTION AT NEW START POINT, WITH IFLAG=4.
START MIGRAD MINIMIZATION. STRATEGY 1. CONVERGENCE WHEN EDM .LT. 1.00e-03
FCN=2766.64 FROM MIGRAD STATUS=INITIATE 6 CALLS 7 TOTAL
EDM= unknown STRATEGY= 1 NO ERROR MATRIX
EXT PARAMETER CURRENT GUESS STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 a1 -4.85553e-03 3.00247e-02 3.00296e-02 -1.97827e+01
2 a2 9.86520e-02 2.98987e-02 3.06116e-02 -1.19823e+01
ERR DEF= 0.5
MIGRAD MINIMIZATION HAS CONVERGED.
MIGRAD WILL VERIFY CONVERGENCE AND ERROR MATRIX.
COVARIANCE MATRIX CALCULATED SUCCESSFULLY
FCN=2766.49 FROM MIGRAD STATUS=CONVERGED 29 CALLS 30 TOTAL
EDM=7.62783e-07 STRATEGY= 1 ERROR MATRIX ACCURATE
EXT PARAMETER STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 a1 8.94396e-03 2.69244e-02 9.81558e-04 3.18558e-02
2 a2 1.01291e-01 1.67455e-02 6.10755e-04 -9.73691e-03
ERR DEF= 0.5
EXTERNAL ERROR MATRIX. NDIM= 25 NPAR= 2 ERR DEF=0.5
7.251e-04 -6.220e-07
-6.220e-07 2.804e-04
PARAMETER CORRELATION COEFFICIENTS
NO. GLOBAL 1 2
1 0.00138 1.000 -0.001
2 0.00138 -0.001 1.000
**********
** 28 **SET ERR 0.5
**********
**********
** 29 **SET PRINT 1
**********
**********
** 30 **HESSE 1000
**********
COVARIANCE MATRIX CALCULATED SUCCESSFULLY
FCN=2766.49 FROM HESSE STATUS=OK 10 CALLS 40 TOTAL
EDM=7.63714e-07 STRATEGY= 1 ERROR MATRIX ACCURATE
EXT PARAMETER INTERNAL INTERNAL
NO. NAME VALUE ERROR STEP SIZE VALUE
1 a1 8.94396e-03 2.69247e-02 1.96312e-04 8.94408e-03
2 a2 1.01291e-01 1.67458e-02 2.44302e-05 -1.36917e+00
ERR DEF= 0.5
EXTERNAL ERROR MATRIX. NDIM= 25 NPAR= 2 ERR DEF=0.5
7.251e-04 -2.218e-06
-2.218e-06 2.804e-04
PARAMETER CORRELATION COEFFICIENTS
NO. GLOBAL 1 2
1 0.00492 1.000 -0.005
2 0.00492 -0.005 1.000
[#1] INFO:Minization -- RooMinimizer::optimizeConst: deactivating const optimization
[#1] INFO:Minization -- RooMinimizer::optimizeConst: activating const optimization
**********
** 31 **SET PRINT 1
**********
**********
** 32 **SET NOGRAD
**********
PARAMETER DEFINITIONS:
NO. NAME VALUE STEP SIZE LIMITS
1 a1 8.94396e-03 2.69247e-02 -1.00000e+00 1.00000e+00
2 a2 1.01291e-01 1.67458e-02 0.00000e+00 1.00000e+01
**********
** 33 **SET ERR 0.5
**********
**********
** 34 **SET PRINT 1
**********
**********
** 35 **SET STR 1
**********
NOW USING STRATEGY 1: TRY TO BALANCE SPEED AGAINST RELIABILITY
**********
** 36 **MIGRAD 1000 1
**********
FIRST CALL TO USER FUNCTION AT NEW START POINT, WITH IFLAG=4.
START MIGRAD MINIMIZATION. STRATEGY 1. CONVERGENCE WHEN EDM .LT. 1.00e-03
FCN=118896 FROM MIGRAD STATUS=INITIATE 8 CALLS 9 TOTAL
EDM= unknown STRATEGY= 1 NO ERROR MATRIX
EXT PARAMETER CURRENT GUESS STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 a1 8.94396e-03 2.69247e-02 2.69290e-02 5.93783e+02
2 a2 1.01291e-01 1.67458e-02 1.67812e-02 5.89498e+02
ERR DEF= 0.5
MIGRAD MINIMIZATION HAS CONVERGED.
MIGRAD WILL VERIFY CONVERGENCE AND ERROR MATRIX.
COVARIANCE MATRIX CALCULATED SUCCESSFULLY
FCN=118892 FROM MIGRAD STATUS=CONVERGED 30 CALLS 31 TOTAL
EDM=2.21121e-06 STRATEGY= 1 ERROR MATRIX ACCURATE
EXT PARAMETER STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 a1 -1.13263e-03 4.02053e-03 9.57731e-04 8.59142e-02
2 a2 9.75516e-02 2.36606e-03 5.73586e-04 -5.99867e-01
ERR DEF= 0.5
EXTERNAL ERROR MATRIX. NDIM= 25 NPAR= 2 ERR DEF=0.5
1.616e-05 -6.207e-08
-6.207e-08 5.598e-06
PARAMETER CORRELATION COEFFICIENTS
NO. GLOBAL 1 2
1 0.00652 1.000 -0.007
2 0.00652 -0.007 1.000
**********
** 37 **SET ERR 0.5
**********
**********
** 38 **SET PRINT 1
**********
**********
** 39 **HESSE 1000
**********
COVARIANCE MATRIX CALCULATED SUCCESSFULLY
FCN=118892 FROM HESSE STATUS=OK 10 CALLS 41 TOTAL
EDM=2.21254e-06 STRATEGY= 1 ERROR MATRIX ACCURATE
EXT PARAMETER INTERNAL INTERNAL
NO. NAME VALUE ERROR STEP SIZE VALUE
1 a1 -1.13263e-03 4.02065e-03 1.91546e-04 -1.13263e-03
2 a2 9.75516e-02 2.36614e-03 2.29434e-05 -1.37294e+00
ERR DEF= 0.5
EXTERNAL ERROR MATRIX. NDIM= 25 NPAR= 2 ERR DEF=0.5
1.617e-05 -9.497e-08
-9.497e-08 5.599e-06
PARAMETER CORRELATION COEFFICIENTS
NO. GLOBAL 1 2
1 0.00998 1.000 -0.010
2 0.00998 -0.010 1.000
[#1] INFO:Minization -- RooMinimizer::optimizeConst: deactivating const optimization
DataStore pxData_binned (Generated From px_binned)
Contains 40 entries
Observables:
1) x = -1.26187 L(-10 - 10) B(40) "x"
Binned Dataset pxData_binned (Generated From px_binned)
Contains 40 bins with a total weight of 43238.9
Observables: 1) x = -1.26187 L(-10 - 10) B(40) "x"
**********
** 40 **SET PRINT 1
**********
**********
** 41 **SET NOGRAD
**********
PARAMETER DEFINITIONS:
NO. NAME VALUE STEP SIZE LIMITS
1 a1 -1.13263e-03 4.02065e-03 -1.00000e+00 1.00000e+00
2 a2 9.75516e-02 2.36614e-03 0.00000e+00 1.00000e+01
**********
** 42 **SET ERR 1
**********
**********
** 43 **SET PRINT 1
**********
**********
** 44 **SET STR 1
**********
NOW USING STRATEGY 1: TRY TO BALANCE SPEED AGAINST RELIABILITY
**********
** 45 **MIGRAD 1000 1
**********
FIRST CALL TO USER FUNCTION AT NEW START POINT, WITH IFLAG=4.
START MIGRAD MINIMIZATION. STRATEGY 1. CONVERGENCE WHEN EDM .LT. 1.00e-03
FCN=32.3464 FROM MIGRAD STATUS=INITIATE 6 CALLS 7 TOTAL
EDM= unknown STRATEGY= 1 NO ERROR MATRIX
EXT PARAMETER CURRENT GUESS STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 a1 -1.13263e-03 4.02065e-03 4.02066e-03 2.74413e+01
2 a2 9.75516e-02 2.36614e-03 2.40760e-03 -2.04371e+02
MIGRAD MINIMIZATION HAS CONVERGED.
MIGRAD WILL VERIFY CONVERGENCE AND ERROR MATRIX.
COVARIANCE MATRIX CALCULATED SUCCESSFULLY
FCN=31.3747 FROM MIGRAD STATUS=CONVERGED 28 CALLS 29 TOTAL
EDM=8.52339e-08 STRATEGY= 1 ERROR MATRIX ACCURATE
EXT PARAMETER STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 a1 -9.98900e-03 2.62975e-02 7.27538e-05 4.94399e-03
2 a2 1.06373e-01 1.01849e-02 2.73457e-05 -3.91519e-02
EXTERNAL ERROR MATRIX. NDIM= 25 NPAR= 2 ERR DEF=1
6.917e-04 -6.529e-06
-6.529e-06 1.037e-04
PARAMETER CORRELATION COEFFICIENTS
NO. GLOBAL 1 2
1 0.02437 1.000 -0.024
2 0.02437 -0.024 1.000
**********
** 46 **SET ERR 1
**********
**********
** 47 **SET PRINT 1
**********
**********
** 48 **HESSE 1000
**********
COVARIANCE MATRIX CALCULATED SUCCESSFULLY
FCN=31.3747 FROM HESSE STATUS=OK 10 CALLS 39 TOTAL
EDM=8.52317e-08 STRATEGY= 1 ERROR MATRIX ACCURATE
EXT PARAMETER INTERNAL INTERNAL
NO. NAME VALUE ERROR STEP SIZE VALUE
1 a1 -9.98900e-03 2.62976e-02 1.45508e-05 -9.98917e-03
2 a2 1.06373e-01 1.01850e-02 5.46914e-06 -1.36415e+00
EXTERNAL ERROR MATRIX. NDIM= 25 NPAR= 2 ERR DEF=1
6.917e-04 -6.575e-06
-6.575e-06 1.037e-04
PARAMETER CORRELATION COEFFICIENTS
NO. GLOBAL 1 2
1 0.02455 1.000 -0.025
2 0.02455 -0.025 1.000
==> ML Fit results on 1K unweighted events
RooFitResult: minimized FCN value: 2766.49, estimated distance to minimum: 7.63714e-07
covariance matrix quality: Full, accurate covariance matrix
Status : MINIMIZE=0 HESSE=0
Floating Parameter FinalValue +/- Error
-------------------- --------------------------
a1 8.9440e-03 +/- 2.69e-02
a2 1.0129e-01 +/- 1.67e-02
==> ML Fit results on 43K unweighted events
RooFitResult: minimized FCN value: 118892, estimated distance to minimum: 2.21254e-06
covariance matrix quality: Full, accurate covariance matrix
Status : MINIMIZE=0 HESSE=0
Floating Parameter FinalValue +/- Error
-------------------- --------------------------
a1 -1.1326e-03 +/- 4.02e-03
a2 9.7552e-02 +/- 2.37e-03
==> ML Fit results on 1K weighted events with a summed weight of 43K
RooFitResult: minimized FCN value: 119682, estimated distance to minimum: 1.28662e-07
covariance matrix quality: Full, accurate covariance matrix
Status : MINIMIZE=0 HESSE=0
Floating Parameter FinalValue +/- Error
-------------------- --------------------------
a1 -4.8560e-03 +/- 4.03e-03
a2 9.8651e-02 +/- 2.41e-03
==> Corrected ML Fit results on 1K weighted events with a summed weight of 43K
RooFitResult: minimized FCN value: 6.84247e+06, estimated distance to minimum: 158914
covariance matrix quality: Unknown, matrix was externally provided
Status : MINIMIZE=0 HESSE=0 HESSE=0
Floating Parameter FinalValue +/- Error
-------------------- --------------------------
a1 -4.8555e-03 +/- 3.00e-02
a2 9.8652e-02 +/- 2.99e-02
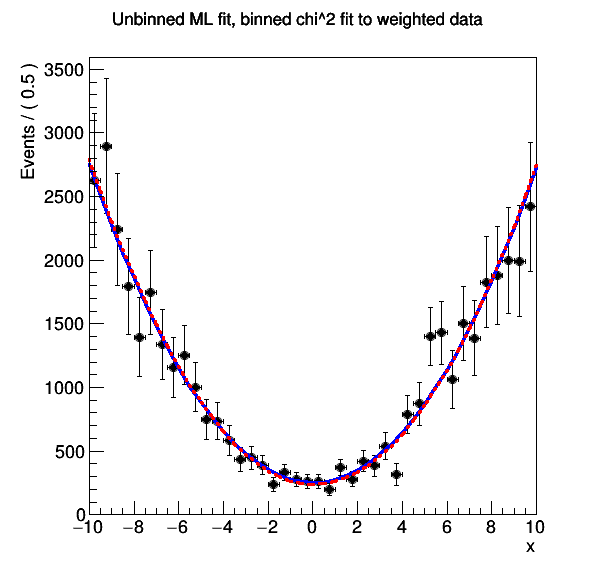
==> Chi2 Fit results on 1K weighted events with a summed weight of 43K
RooFitResult: minimized FCN value: 31.3747, estimated distance to minimum: 8.52317e-08
covariance matrix quality: Full, accurate covariance matrix
Status : MIGRAD=0 HESSE=0
Floating Parameter FinalValue +/- Error
-------------------- --------------------------
a1 -9.9890e-03 +/- 2.63e-02
a2 1.0637e-01 +/- 1.02e-02
#include "RooRealVar.h"
#include "RooDataSet.h"
#include "RooDataHist.h"
#include "RooGaussian.h"
#include "RooConstVar.h"
#include "RooFormulaVar.h"
#include "RooGenericPdf.h"
#include "RooPolynomial.h"
#include "RooChi2Var.h"
#include "RooMinimizer.h"
#include "TCanvas.h"
#include "TAxis.h"
#include "RooPlot.h"
#include "RooFitResult.h"
using namespace RooFit ;
void rf403_weightedevts()
{
// C r e a t e o b s e r v a b l e a n d u n w e i g h t e d d a t a s e t
// -------------------------------------------------------------------------------
// Declare observable
RooRealVar x("x","x",-10,10) ;
x.setBins(40) ;
// Construction a uniform pdf
RooPolynomial p0("px","px",x) ;
// Sample 1000 events from pdf
RooDataSet* data = p0.generate(x,1000) ;
// C a l c u l a t e w e i g h t a n d m a k e d a t a s e t w e i g h t e d
// -----------------------------------------------------------------------------------
// Construct formula to calculate (fake) weight for events
RooFormulaVar wFunc("w","event weight","(x*x+10)",x) ;
// Add column with variable w to previously generated dataset
RooRealVar* w = (RooRealVar*) data->addColumn(wFunc) ;
// Dataset d is now a dataset with two observable (x,w) with 1000 entries
data->Print() ;
// Instruct dataset wdata in interpret w as event weight rather than as observable
RooDataSet wdata(data->GetName(),data->GetTitle(),data,*data->get(),0,w->GetName()) ;
// Dataset d is now a dataset with one observable (x) with 1000 entries and a sum of weights of ~430K
wdata.Print() ;
// U n b i n n e d M L f i t t o w e i g h t e d d a t a
// ---------------------------------------------------------------
// Construction quadratic polynomial pdf for fitting
RooRealVar a0("a0","a0",1) ;
RooRealVar a1("a1","a1",0,-1,1) ;
RooRealVar a2("a2","a2",1,0,10) ;
RooPolynomial p2("p2","p2",x,RooArgList(a0,a1,a2),0) ;
// Fit quadratic polynomial to weighted data
// NOTE: A plain Maximum likelihood fit to weighted data does in general
// NOT result in correct error estimates, unless individual
// event weights represent Poisson statistics themselves.
//
// Fit with 'wrong' errors
RooFitResult* r_ml_wgt = p2.fitTo(wdata,Save()) ;
// A first order correction to estimated parameter errors in an
// (unbinned) ML fit can be obtained by calculating the
// covariance matrix as
//
// V' = V C-1 V
//
// where V is the covariance matrix calculated from a fit
// to -logL = - sum [ w_i log f(x_i) ] and C is the covariance
// matrix calculated from -logL' = -sum [ w_i^2 log f(x_i) ]
// (i.e. the weights are applied squared)
//
// A fit in this mode can be performed as follows:
RooFitResult* r_ml_wgt_corr = p2.fitTo(wdata,Save(),SumW2Error(kTRUE)) ;
// P l o t w e i g h e d d a t a a n d f i t r e s u l t
// ---------------------------------------------------------------
// Construct plot frame
RooPlot* frame = x.frame(Title("Unbinned ML fit, binned chi^2 fit to weighted data")) ;
// Plot data using sum-of-weights-squared error rather than Poisson errors
wdata.plotOn(frame,DataError(RooAbsData::SumW2)) ;
// Overlay result of 2nd order polynomial fit to weighted data
p2.plotOn(frame) ;
// ML Fit of pdf to equivalent unweighted dataset
// -----------------------------------------------------------------------------------------
// Construct a pdf with the same shape as p0 after weighting
RooGenericPdf genPdf("genPdf","x*x+10",x) ;
// Sample a dataset with the same number of events as data
RooDataSet* data2 = genPdf.generate(x,1000) ;
// Sample a dataset with the same number of weights as data
RooDataSet* data3 = genPdf.generate(x,43000) ;
// Fit the 2nd order polynomial to both unweighted datasets and save the results for comparison
RooFitResult* r_ml_unw10 = p2.fitTo(*data2,Save()) ;
RooFitResult* r_ml_unw43 = p2.fitTo(*data3,Save()) ;
// C h i 2 f i t o f p d f t o b i n n e d w e i g h t e d d a t a s e t
// ------------------------------------------------------------------------------------
// Construct binned clone of unbinned weighted dataset
RooDataHist* binnedData = wdata.binnedClone() ;
binnedData->Print("v") ;
// Perform chi2 fit to binned weighted dataset using sum-of-weights errors
//
// NB: Within the usual approximations of a chi2 fit, a chi2 fit to weighted
// data using sum-of-weights-squared errors does give correct error
// estimates
RooChi2Var chi2("chi2","chi2",p2,*binnedData,DataError(RooAbsData::SumW2)) ;
RooMinimizer m(chi2) ;
m.migrad() ;
m.hesse() ;
// Plot chi^2 fit result on frame as well
RooFitResult* r_chi2_wgt = m.save() ;
p2.plotOn(frame,LineStyle(kDashed),LineColor(kRed)) ;
// C o m p a r e f i t r e s u l t s o f c h i 2 , M L f i t s t o ( u n ) w e i g h t e d d a t a
// ---------------------------------------------------------------------------------------------------------------
// Note that ML fit on 1Kevt of weighted data is closer to result of ML fit on 43Kevt of unweighted data
// than to 1Kevt of unweighted data, whereas the reference chi^2 fit with SumW2 error gives a result closer to
// that of an unbinned ML fit to 1Kevt of unweighted data.
cout << "==> ML Fit results on 1K unweighted events" << endl ;
r_ml_unw10->Print() ;
cout << "==> ML Fit results on 43K unweighted events" << endl ;
r_ml_unw43->Print() ;
cout << "==> ML Fit results on 1K weighted events with a summed weight of 43K" << endl ;
r_ml_wgt->Print() ;
cout << "==> Corrected ML Fit results on 1K weighted events with a summed weight of 43K" << endl ;
r_ml_wgt_corr->Print() ;
cout << "==> Chi2 Fit results on 1K weighted events with a summed weight of 43K" << endl ;
r_chi2_wgt->Print() ;
new TCanvas("rf403_weightedevts","rf403_weightedevts",600,600) ;
gPad->SetLeftMargin(0.15) ; frame->GetYaxis()->SetTitleOffset(1.8) ; frame->Draw() ;
}
Author
07/2008 - Wouter Verkerke

Definition in file rf403_weightedevts.C.