mlpRegression.C File Reference

Detailed Description

This macro shows the use of an ANN for regression analysis: given a set {i} of input vectors i and a set {o} of output vectors o, one looks for the unknown function f(i)=o.

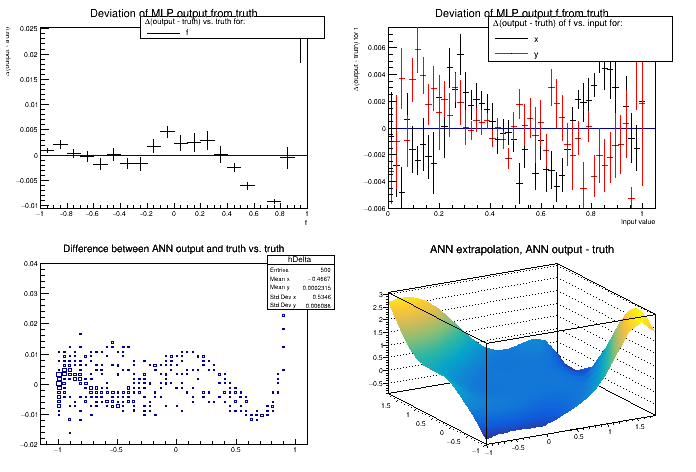
The ANN can approximate this function; TMLPAnalyzer::DrawTruthDeviation methods can be used to evaluate the quality of the approximation.

For simplicity, we use a known function to create test and training data. In reality this function is usually not known, and the data comes e.g. from measurements.

Processing /mnt/build/workspace/root-makedoc-v610/rootspi/rdoc/src/v6-10-00-patches/tutorials/mlp/mlpRegression.C...
Network with structure: x,y:10:8:f
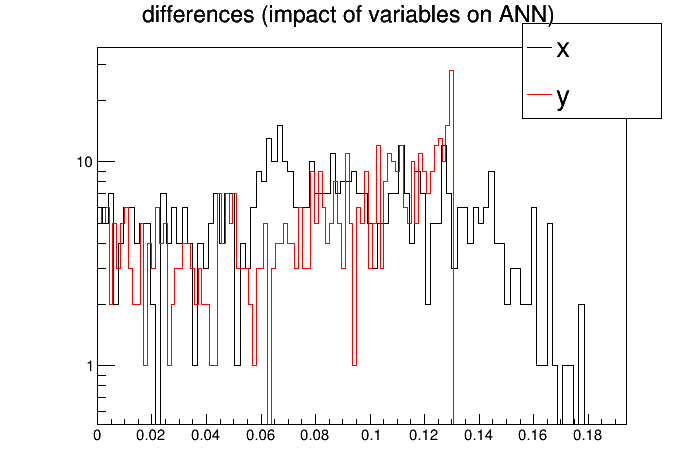
inputs with low values in the differences plot may not be needed
x -> 0.0836825 +/- 0.0431364
y -> 0.0812535 +/- 0.0399349

Double_t theUnknownFunction(Double_t x, Double_t y) {
   return sin((1.7+x)*(x-0.3)-2.3*(y+0.7));
}

void mlpRegression() {
   // create a tree with train and test data.
   // we have two input parameters x and y,
   // and one output value f(x,y)
   TNtuple* t=new TNtuple("tree","tree","x:y:f");
   TRandom r;
   for (Int_t i=0; i<1000; i++) {
      Float_t x=r.Rndm();
      Float_t y=r.Rndm();
      // fill it with x, y, and f(x,y) - usually this function
      // is not known, and the value of f given an x and a y comes
      // e.g. from measurements
      t->Fill(x,y,theUnknownFunction(x,y));
   }

   // create ANN
   TMultiLayerPerceptron* mlp=new TMultiLayerPerceptron("x,y:10:8:f",t,
      "Entry$%2","(Entry$%2)==0");
   mlp->Train(150,"graph update=10");

   // analyze it
   TMLPAnalyzer* mlpa=new TMLPAnalyzer(mlp);
   mlpa->GatherInformations();
   mlpa->CheckNetwork();
   mlpa->DrawDInputs();

   // draw statistics shows the quality of the ANN's approximation
   TCanvas* cIO=new TCanvas("TruthDeviation", "TruthDeviation");
   cIO->Divide(2,2);
   cIO->cd(1);
   // draw the difference between the ANN's output for (x,y) and
   // the true value f(x,y), vs. f(x,y), as TProfiles
   mlpa->DrawTruthDeviations();

   cIO->cd(2);
   // draw the difference between the ANN's output for (x,y) and
   // the true value f(x,y), vs. x, and vs. y, as TProfiles
   mlpa->DrawTruthDeviationInsOut();

   cIO->cd(3);
   // draw a box plot of the ANN's output for (x,y) vs f(x,y)
   mlpa->GetIOTree()->Draw("Out.Out0-True.True0:True.True0>>hDelta","","goff");
   TH2F* hDelta=(TH2F*)gDirectory->Get("hDelta");
   hDelta->SetTitle("Difference between ANN output and truth vs. truth");
   hDelta->Draw("BOX");

   cIO->cd(4);
   // draw difference of ANN's output for (x,y) vs f(x,y) assuming
   // the ANN can extrapolate
   Double_t vx[225];
   Double_t vy[225];
   Double_t delta[225];
   Double_t v[2];
   for (Int_t ix=0; ix<15; ix++) {
      v[0]=ix/5.-1.;
      for (Int_t iy=0; iy<15; iy++) {
         v[1]=iy/5.-1.;
         Int_t idx=ix*15+iy;
         vx[idx]=v[0];
         vy[idx]=v[1];
         delta[idx]=mlp->Evaluate(0, v)-theUnknownFunction(v[0],v[1]);
      }
   }
   TGraph2D* g2Extrapolate=new TGraph2D("ANN extrapolation",
                                        "ANN extrapolation, ANN output - truth",
                                        225, vx, vy, delta);

   g2Extrapolate->Draw("TRI2");
}

Author

Axel Naumann, 2005-02-02

Definition in file mlpRegression.C.