candleplotwhiskers.C File Reference

Detailed Description

Example of candle plot showing the whiskers definition.

Processing /mnt/build/workspace/root-makedoc-v610/rootspi/rdoc/src/v6-10-00-patches/tutorials/hist/candleplotwhiskers.C...
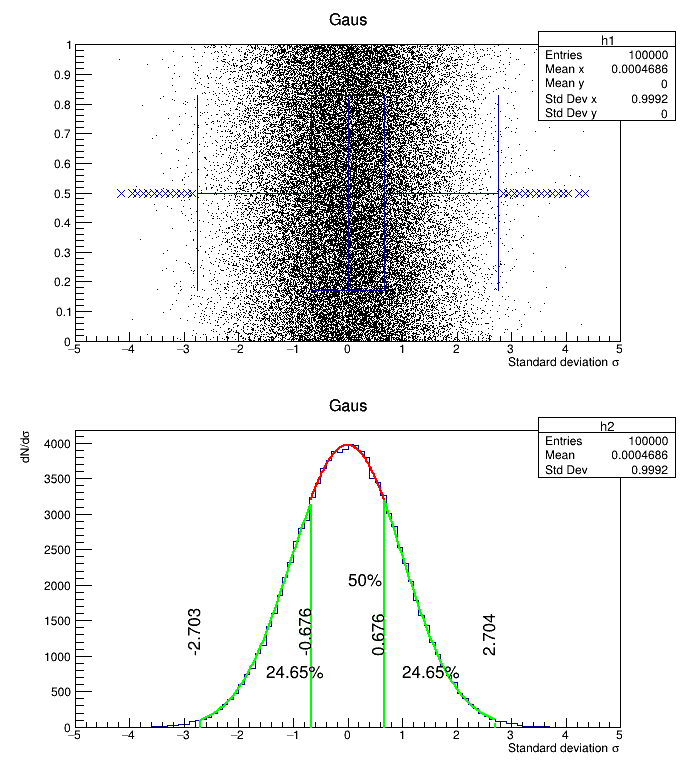
Q1 (-25%): -0.675525 Median: 0.00168511 Q3 (+25%): 0.676189
 FCN=11.7941 FROM MIGRAD    STATUS=CONVERGED     138 CALLS         139 TOTAL
                     EDM=1.08103e-12    STRATEGY= 1      ERROR MATRIX ACCURATE 
  EXT PARAMETER                                   STEP         FIRST   
  NO.   NAME      VALUE            ERROR          SIZE      DERIVATIVE 
   1  Constant     3.72831e+03   1.82107e+02   4.21637e-02   1.36245e-08
   2  Mean        -1.10774e-01   7.20921e-02   8.42717e-06  -1.49401e-04
   3  Sigma        9.59469e-01   2.51499e-02   2.82317e-06   5.37129e-04
 FCN=8.04689 FROM MIGRAD    STATUS=CONVERGED     139 CALLS         140 TOTAL
                     EDM=6.08152e-08    STRATEGY= 1      ERROR MATRIX ACCURATE 
  EXT PARAMETER                                   STEP         FIRST   
  NO.   NAME      VALUE            ERROR          SIZE      DERIVATIVE 
   1  Constant     4.07186e+03   2.44580e+02   3.87026e-02   3.94837e-07
   2  Mean        -2.92179e-02   8.71835e-02   7.07837e-06  -2.13598e-02
   3  Sigma        1.00971e+00   2.88317e-02   2.27510e-06  -1.25158e-01
 FCN=6.93238 FROM MIGRAD    STATUS=CONVERGED     106 CALLS         107 TOTAL
                     EDM=6.56099e-08    STRATEGY= 1      ERROR MATRIX ACCURATE 
  EXT PARAMETER                                   STEP         FIRST   
  NO.   NAME      VALUE            ERROR          SIZE      DERIVATIVE 
   1  Constant     3.97002e+03   2.57596e+01   2.40433e-02  -9.00146e-06
   2  Mean        -1.89022e-04   1.18284e-02   1.62701e-05   7.29142e-03
   3  Sigma        1.02465e+00   3.35469e-02   1.82218e-05   7.40149e-03

void candleplotwhiskers() {
   TCanvas *c1 = new TCanvas("c1","Candle Presets",700,800);
   c1->Divide(1,2);

   TRandom *randnum = new TRandom();
   TH2I *h1 = new TH2I("h1","Gaus",100,-5,5,1,0,1);
   TH1I *h2 = new TH1I("h2","Gaus",100,-5,5);

   h1->GetXaxis()->SetTitle("Standard deviation #sigma");
   h2->GetXaxis()->SetTitle("Standard deviation #sigma");
   h2->GetYaxis()->SetTitle("dN/d#sigma");

   float myRand;
   for (int i = 0; i < 100000; i++) {
       myRand = randnum->Gaus(0,1);
       h1->Fill(myRand,0);
       h2->Fill(myRand);
   }

   Double_t *q = new Double_t[3];
   Double_t *p = new Double_t[3];
   q[0] = 0.; q[1] = 0.; q[2] = 0.;
   p[0] = 0.25; p[1] = 0.5; p[2] = 0.75;

   h2->GetQuantiles(3,q,p);
   cout << "Q1 (-25%): " << q[0] << " Median: " << q[1] << " Q3 (+25%): " << q[2] << endl;
   double iqr = q[2]-q[0];
   TF1 *mygaus_1_middle = new TF1("mygaus_1_middle","gaus",q[0],q[2]);
   TF1 *mygaus_1_left   = new TF1("mygaus_1_left","gaus",q[0]-1.5*iqr,q[0]);
   mygaus_1_left->SetLineColor(kGreen);
   TF1 *mygaus_1_right  = new TF1("mygaus_1_right","gaus",q[2],q[2]+1.5*iqr);
   mygaus_1_right->SetLineColor(kGreen);
   c1->cd(1);
   h1->SetLineWidth(3);
   h1->SetFillStyle(0);
   h1->Draw("candley2 scat");

   c1->cd(2);
   h2->Draw("");
   h2->Fit("mygaus_1_left","R");
   mygaus_1_left->Draw("same");
   TLine *l3 = new TLine(q[0]-1.5*iqr,0,q[0]-1.5*iqr,mygaus_1_left->Eval(q[0]-1.5*iqr));
   l3->SetLineColor(kGreen); l3->SetLineWidth(2);      l3->Draw("");
   TLine *l1 = new TLine(q[0]        ,0,q[0]        ,mygaus_1_left->Eval(q[0]));
   l1->SetLineWidth(2);      l1->SetLineColor(kGreen); l1->Draw("");

   h2->Fit("mygaus_1_right","R","");
   mygaus_1_right->Draw("same");
   TLine *l4 = new TLine(q[2]+1.5*iqr,0,q[2]+1.5*iqr,mygaus_1_left->Eval(q[2]+1.5*iqr));
   l4->SetLineColor(kGreen); l4->SetLineWidth(2);      l4->Draw("");
   TLine *l5 = new TLine(q[2]        ,0,q[2]        ,mygaus_1_right->Eval(q[2]));
   l5->SetLineWidth(2);      l5->SetLineColor(kGreen); l5->Draw("");

   h2->Fit("mygaus_1_middle","R");
   mygaus_1_middle->Draw("same");

   //In principal one could calculate these values by h2->Integral() as well
   TText *t = new TText(); t->SetTextFont(42);
   t->DrawText(0,mygaus_1_middle->Eval(0)/2,"50%");
   t->DrawText(-1.5,mygaus_1_middle->Eval(-1.5)/2,"24.65%");
   t->DrawText(+1,mygaus_1_middle->Eval(+1.5)/2,"24.65%");
   t->DrawText(q[0]-1.5*iqr,1000,Form("%.3f",q[0]-1.5*iqr))->SetTextAngle(90);
   t->DrawText(q[2]+1.5*iqr,1000,Form("%.3f",q[2]+1.5*iqr))->SetTextAngle(90);
   t->DrawText(q[0],1000,Form("%.3f",q[0]))->SetTextAngle(90);
   t->DrawText(q[2],1000,Form("%.3f",q[2]))->SetTextAngle(90);
}

Author

Georg Troska

Definition in file candleplotwhiskers.C.