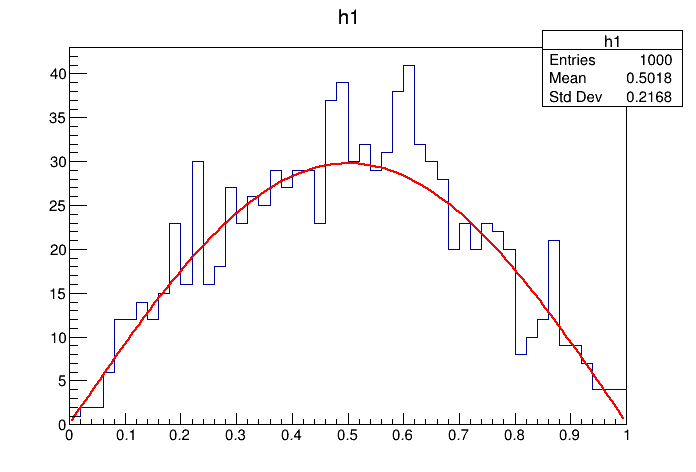
Estimate the error in the integral of a fitted function taking into account the errors in the parameters resulting from the fit.
Estimate the error in the integral of a fitted function taking into account the errors in the parameters resulting from the fit.
The error is estimated also using the correlations values obtained from the fit
run the macro doing:
Processing /mnt/build/workspace/root-makedoc-v610/rootspi/rdoc/src/v6-10-00-patches/tutorials/fit/ErrorIntegral.C...
FCN=49.5952 FROM MIGRAD STATUS=CONVERGED 52 CALLS 53 TOTAL
EDM=1.22682e-09 STRATEGY= 1 ERROR MATRIX UNCERTAINTY 2.5 per cent
EXT PARAMETER STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 p0 3.13201e+00 3.12699e-02 -3.64656e-05 2.15221e-03
2 p1 2.97626e+01 1.00773e+00 6.67621e-05 -4.02033e-06
Integral = 19.005 +/- 0.6159
#include <assert.h>
#include <iostream>
#include <cmath>
const int NPAR = 2;
double f(
double * x,
double * p) {
}
void ErrorIntegral() {
fitFunc =
new TF1(
"f",f,0,1,NPAR);
double par[NPAR] = { 3.14, 1.};
double integral = fitFunc->
Integral(0,1);
assert(fitter != 0);
std::cout << "Integral = " << integral << " +/- " << sigma_integral
<< std::endl;
double ic = p[1]* (1-
std::cos(p[0]) )/p[0];
double sic =
std::sqrt( c0c*c0c * covMatrix[0] + c1c*c1c * covMatrix[3]
+ 2.* c0c*c1c * covMatrix[1]);
if (
std::fabs(sigma_integral-sic) > 1.E-6*sic )
std::cout << " ERROR: test failed : different analytical integral : "
<< ic << " +/- " << sic << std::endl;
}
- Author
- Lorenzo Moneta
Definition in file ErrorIntegral.C.



 Estimate the error in the integral of a fitted function taking into account the errors in the parameters resulting from the fit.
Estimate the error in the integral of a fitted function taking into account the errors in the parameters resulting from the fit.