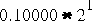 and
and 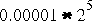 are just two unnormalized representations of the value 1.
are just two unnormalized representations of the value 1.
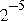 apart, while numbers just smaller than 1 are spaced half as far apart. In fact, the normal powers of 2 divide the number system into binades, the binary analog of decades. Numbers in the binade below a power of two are spaced half as far apart as numbers in the binade above. Figure 54 is a picture of the situation near 1.
apart, while numbers just smaller than 1 are spaced half as far apart. In fact, the normal powers of 2 divide the number system into binades, the binary analog of decades. Numbers in the binade below a power of two are spaced half as far apart as numbers in the binade above. Figure 54 is a picture of the situation near 1.
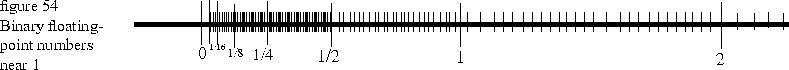
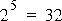 members, including the leftmost power of 2.
members, including the leftmost power of 2.

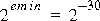 . It is possible to represent even smaller values by admitting unnormalized values with the same exponent, emin. The IEEE binary floating-point arithmetic standard introduced these values as denormalized; the more modern term is subnormal.
. It is possible to represent even smaller values by admitting unnormalized values with the same exponent, emin. The IEEE binary floating-point arithmetic standard introduced these values as denormalized; the more modern term is subnormal.
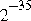 , is the smallest subnormal number. (On most pre-IEEE platforms, this teeny difference would underflow to zero.)
, is the smallest subnormal number. (On most pre-IEEE platforms, this teeny difference would underflow to zero.)
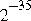 in this case). Subnormal numbers reach all the way to zero because they have the same spacing as the normal numbers in the smallest binade. Figure 55
in this case). Subnormal numbers reach all the way to zero because they have the same spacing as the normal numbers in the smallest binade. Figure 55
Units in the
last place
In the context of numbers of a specific precision, it's useful to speak of rounding and other phenomena in terms of ulps (units in the last place of a specific value). For example, one ulp of 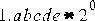 , where abcde is any 5-bit sequence,
, where abcde is any 5-bit sequence,
is 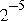 . One ulp of
. One ulp of 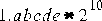 is
is 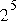 . One ulp of the subnormal value
. One ulp of the subnormal value 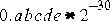 is
is 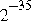 .
.
[Contents]
[Previous]
[Next]
![]() Click the icon to mail questions or corrections about this material to Taligent personnel.
Click the icon to mail questions or corrections about this material to Taligent personnel.