// @(#)root/geom:$Name:  $:$Id: TGeoPara.cxx,v 1.29 2005/11/18 16:07:58 brun Exp $
// Author: Andrei Gheata   31/01/02
// TGeoPara::Contains() implemented by Mihaela Gheata

/*************************************************************************
 * Copyright (C) 1995-2000, Rene Brun and Fons Rademakers.               *
 * All rights reserved.                                                  *
 *                                                                       *
 * For the licensing terms see $ROOTSYS/LICENSE.                         *
 * For the list of contributors see $ROOTSYS/README/CREDITS.             *
 *************************************************************************/

//_____________________________________________________________________________
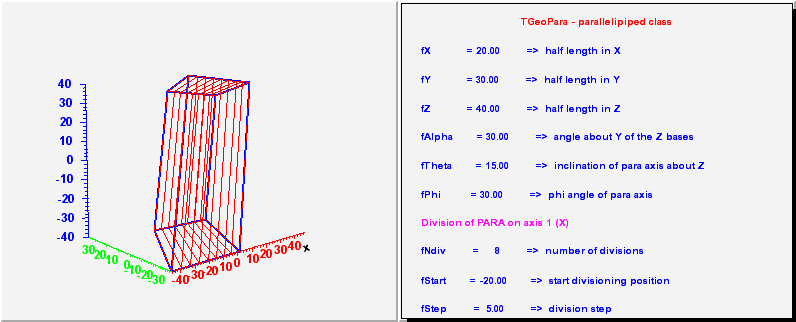
// TGeoPara - parallelipeped class. It has 6 parameters :
//         dx, dy, dz - half lengths in X, Y, Z
//         alpha - angle w.r.t the Y axis from center of low Y edge to
//                 center of high Y edge [deg]
//         theta, phi - polar and azimuthal angles of the segment between
//                 low and high Z surfaces [deg]
//
//_____________________________________________________________________________
//
//

//

//

//

#include "Riostream.h"
#include "TROOT.h"

#include "TGeoManager.h"
#include "TGeoVolume.h"
#include "TGeoPara.h"

ClassImp(TGeoPara)
   
//_____________________________________________________________________________
 TGeoPara::TGeoPara()
{
// Default constructor
   SetShapeBit(TGeoShape::kGeoPara);
   fX = fY = fZ = 0;
   fAlpha = 0;
   fTheta = 0;
   fPhi = 0;
   fTxy = 0;
   fTxz = 0;
   fTyz = 0;
}   

//_____________________________________________________________________________
 TGeoPara::TGeoPara(Double_t dx, Double_t dy, Double_t dz, Double_t alpha,
                   Double_t theta, Double_t phi)
           :TGeoBBox(0, 0, 0)
{
// Default constructor specifying minimum and maximum radius
   SetShapeBit(TGeoShape::kGeoPara);
   fX = dx;
   fY = dy;
   fZ = dz;
   fAlpha = alpha;
   fTheta = theta;
   fPhi = phi;
   fTxy = TMath::Tan(alpha*TMath::DegToRad());
   Double_t tth = TMath::Tan(theta*TMath::DegToRad());
   Double_t ph  = phi*TMath::DegToRad();
   fTxz = tth*TMath::Cos(ph);
   fTyz = tth*TMath::Sin(ph);
   if ((fX<0) || (fY<0) || (fZ<0)) {
//      printf("para : %f %f %f\n", fX, fY, fZ);
      SetShapeBit(kGeoRunTimeShape);
   }
   else ComputeBBox();
}

//_____________________________________________________________________________
 TGeoPara::TGeoPara(const char *name, Double_t dx, Double_t dy, Double_t dz, Double_t alpha,
                   Double_t theta, Double_t phi)
           :TGeoBBox(name, 0, 0, 0)
{
// Default constructor specifying minimum and maximum radius
   SetShapeBit(TGeoShape::kGeoPara);
   fX = dx;
   fY = dy;
   fZ = dz;
   fAlpha = alpha;
   fTheta = theta;
   fPhi = phi;
   fTxy = TMath::Tan(alpha*TMath::DegToRad());
   Double_t tth = TMath::Tan(theta*TMath::DegToRad());
   Double_t ph  = phi*TMath::DegToRad();
   fTxz = tth*TMath::Cos(ph);
   fTyz = tth*TMath::Sin(ph);
   if ((fX<0) || (fY<0) || (fZ<0)) {
//      printf("para : %f %f %f\n", fX, fY, fZ);
      SetShapeBit(kGeoRunTimeShape);
   }
   else ComputeBBox();
}

//_____________________________________________________________________________
 TGeoPara::TGeoPara(Double_t *param)
           :TGeoBBox(0, 0, 0)
{
// Default constructor
// param[0] = dx
// param[1] = dy
// param[2] = dz
// param[3] = alpha
// param[4] = theta
// param[5] = phi
   SetShapeBit(TGeoShape::kGeoPara);
   SetDimensions(param);
   if ((fX<0) || (fY<0) || (fZ<0)) SetShapeBit(kGeoRunTimeShape);
   else ComputeBBox();
}

//_____________________________________________________________________________
 TGeoPara::~TGeoPara()
{
// destructor
}

//_____________________________________________________________________________
 Double_t TGeoPara::Capacity() const
{
// Computes capacity of the shape in [length^3]
   Double_t capacity = 8.*fX*fY*fZ;
   return capacity;
}      

//_____________________________________________________________________________   
 void TGeoPara::ComputeBBox()
{
// compute bounding box
   Double_t dx = fX+fY*TMath::Abs(fTxy)+fZ*TMath::Abs(fTxz);
   Double_t dy = fY+fZ*TMath::Abs(fTyz);
   Double_t dz = fZ;
   TGeoBBox::SetBoxDimensions(dx, dy, dz);
   memset(fOrigin, 0, 3*sizeof(Double_t));
}   

//_____________________________________________________________________________   
 void TGeoPara::ComputeNormal(Double_t *point, Double_t *dir, Double_t *norm)
{
// Compute normal to closest surface from POINT. 
   Double_t saf[3];
   // distance from point to higher Z face
   saf[0] = TMath::Abs(fZ-TMath::Abs(point[2])); // Z

   Double_t yt = point[1]-fTyz*point[2];      
   saf[1] = TMath::Abs(fY-TMath::Abs(yt));       // Y
   // cos of angle YZ
   Double_t cty = 1.0/TMath::Sqrt(1.0+fTyz*fTyz);

   Double_t xt = point[0]-fTxz*point[2]-fTxy*yt;      
   saf[2] = TMath::Abs(fX-TMath::Abs(xt));       // X
   // cos of angle XZ
   Double_t ctx = 1.0/TMath::Sqrt(1.0+fTxy*fTxy+fTxz*fTxz);
   saf[2] *= ctx;
   saf[1] *= cty;
   Int_t i = TMath::LocMin(3,saf);
   switch (i) {
      case 0:
         norm[0] = norm[1] = 0;
         norm[2] = TMath::Sign(1.,dir[2]);
         return;
      case 1:
         norm[0] = 0;   
         norm[1] = cty;
         norm[2] = - fTyz*cty;
         break;
      case 2:
         norm[0] = TMath::Cos(fTheta*TMath::DegToRad())*TMath::Cos(fAlpha*TMath::DegToRad());
         norm[1] = - TMath::Cos(fTheta*TMath::DegToRad())*TMath::Sin(fAlpha*TMath::DegToRad());
         norm[2] = -TMath::Sin(fTheta*TMath::DegToRad());
   }
   if (norm[0]*dir[0]+norm[1]*dir[1]+norm[2]*dir[2]<0) {
      norm[0] = -norm[0];
      norm[1] = -norm[1];
      norm[2] = -norm[2];
   }         
}

//_____________________________________________________________________________
 Bool_t TGeoPara::Contains(Double_t *point) const
{
// test if point is inside this sphere
   // test Z range
   if (TMath::Abs(point[2]) > fZ) return kFALSE;
   // check X and Y
   Double_t yt=point[1]-fTyz*point[2];
   if (TMath::Abs(yt) > fY) return kFALSE;
   Double_t xt=point[0]-fTxz*point[2]-fTxy*yt;
   if (TMath::Abs(xt) > fX) return kFALSE;
   return kTRUE;
}

//_____________________________________________________________________________
 Double_t TGeoPara::DistFromInside(Double_t *point, Double_t *dir, Int_t iact, Double_t step, Double_t *safe) const
{
// compute distance from inside point to surface of the para
// Boundary safe algorithm.
   if (iact<3 && safe) {
   // compute safety
      *safe = Safety(point, kTRUE);
      if (iact==0) return TGeoShape::Big();
      if (iact==1 && step<*safe) return TGeoShape::Big(); 
   }
   Double_t saf[2];
   Double_t snxt = TGeoShape::Big();
   Double_t s;
   saf[0] = fZ+point[2];
   saf[1] = fZ-point[2];
   if (dir[2]!=0) {
      s = (dir[2]>0)?(saf[1]/dir[2]):(-saf[0]/dir[2]);
      if (s<0) return 0.0;
      if (s<snxt) snxt = s;
   }
   // distance from point to center axis on Y 
   Double_t yt = point[1]-fTyz*point[2];      
   saf[0] = fY+yt;
   saf[1] = fY-yt;
   Double_t dy = dir[1]-fTyz*dir[2];
   if (dy!=0) {
      s = (dy>0)?(saf[1]/dy):(-saf[0]/dy);
      if (s<0) return 0.0;
      if (s<snxt) snxt = s;
   }   
   // distance from point to center axis on X 
   Double_t xt = point[0]-fTxz*point[2]-fTxy*yt;      
   saf[0] = fX+xt;
   saf[1] = fX-xt;
   Double_t dx = dir[0]-fTxz*dir[2]-fTxy*dy;
   if (dx!=0) {
      s = (dx>0)?(saf[1]/dx):(-saf[0]/dx);
      if (s<0) return 0.0;
      if (s<snxt) snxt = s;
   }   
   return snxt;
}

//_____________________________________________________________________________
 Double_t TGeoPara::DistFromOutside(Double_t *point, Double_t *dir, Int_t iact, Double_t step, Double_t *safe) const
{
// compute distance from inside point to surface of the para
   Double_t snxt=TGeoShape::Big();
   if (iact<3 && safe) {
      // compute safe distance
      *safe = Safety(point, kFALSE);
      if (iact==0) return TGeoShape::Big();
      if (iact==1 && step<*safe) return TGeoShape::Big();
   }
   Bool_t in = kTRUE;
   Double_t safz;
   safz = TMath::Abs(point[2])-fZ;
   if (safz>0) {
      // outside Z
      if (point[2]*dir[2]>=0) return TGeoShape::Big();
      in = kFALSE;
   }   
   Double_t yt=point[1]-fTyz*point[2];
   Double_t safy = TMath::Abs(yt)-fY;
   Double_t dy=dir[1]-fTyz*dir[2];   
   if (safy>0) {
      if (yt*dy>=0) return TGeoShape::Big();
      in = kFALSE;
   }   
   Double_t xt=point[0]-fTxy*yt-fTxz*point[2];
   Double_t safx = TMath::Abs(xt)-fX;
   Double_t dx=dir[0]-fTxy*dy-fTxz*dir[2];
   if (safx>0) {
      if (xt*dx>=0) return TGeoShape::Big();
      in = kFALSE;
   }   
   // protection in case point is actually inside
   if (in) {
      if (safz>safx && safz>safy) {
         if (point[2]*dir[2]>0) return TGeoShape::Big();
         return 0.0;
      }
      if (safx>safy) {
         if (xt*dx>0) return TGeoShape::Big();
         return 0.0;
      }
      if (yt*dy>0) return TGeoShape::Big();
      return 0.0;
   }         
   Double_t xnew,ynew,znew;
   if (safz>0) {
      snxt = safz/TMath::Abs(dir[2]);
      xnew = point[0]+snxt*dir[0];
      ynew = point[1]+snxt*dir[1];
      znew = (point[2]>0)?fZ:(-fZ);
      Double_t ytn = ynew-fTyz*znew;
      if (TMath::Abs(ytn)<=fY) {
         Double_t xtn = xnew-fTxy*ytn-fTxz*znew;
         if (TMath::Abs(xtn)<=fX) return snxt;
      }
   }
   if (safy>0) {
      snxt = safy/TMath::Abs(dy);
      znew = point[2]+snxt*dir[2];
      if (TMath::Abs(znew)<=fZ) {
         Double_t ytn = (yt>0)?fY:(-fY);
         xnew = point[0]+snxt*dir[0];
         Double_t xtn = xnew-fTxy*ytn-fTxz*znew;
         if (TMath::Abs(xtn)<=fX) return snxt;
      }
   }
   if (safx>0) {
      snxt = safx/TMath::Abs(dx);
      znew = point[2]+snxt*dir[2];
      if (TMath::Abs(znew)<=fZ) { 
         ynew = point[1]+snxt*dir[1];
         Double_t ytn = ynew-fTyz*znew;
         if (TMath::Abs(ytn)<=fY) return snxt;
      }
   }          
   return TGeoShape::Big();                  
}

//_____________________________________________________________________________
 TGeoVolume *TGeoPara::Divide(TGeoVolume *voldiv, const char *divname, Int_t iaxis, Int_t ndiv, 
                             Double_t start, Double_t step) 
{
//--- Divide this paralelipiped shape belonging to volume "voldiv" into ndiv equal volumes
// called divname, from start position with the given step. Returns pointer
// to created division cell volume. In case a wrong division axis is supplied,
// returns pointer to volume to be divided.
   TGeoShape *shape;           //--- shape to be created
   TGeoVolume *vol;            //--- division volume to be created
   TGeoVolumeMulti *vmulti;    //--- generic divided volume
   TGeoPatternFinder *finder;  //--- finder to be attached
   TString opt = "";           //--- option to be attached
   Double_t end=start+ndiv*step;
   switch (iaxis) {
      case 1:                  //--- divide on X
         shape = new TGeoPara(step/2, fY, fZ,fAlpha,fTheta, fPhi);
         finder = new TGeoPatternParaX(voldiv, ndiv, start, end);
         opt = "X";
         break;
      case 2:                  //--- divide on Y
         shape = new TGeoPara(fX, step/2, fZ, fAlpha, fTheta, fPhi);
         finder = new TGeoPatternParaY(voldiv, ndiv, start, end);
         opt = "Y";
         break;
      case 3:                  //--- divide on Z
         shape = new TGeoPara(fX, fY, step/2, fAlpha, fTheta, fPhi);
         finder = new TGeoPatternParaZ(voldiv, ndiv, start, end);
         opt = "Z";
         break;
      default:
         Error("Divide", "Wrong axis type for division");
         return 0;            
   }
   vol = new TGeoVolume(divname, shape, voldiv->GetMedium());
   vmulti = gGeoManager->MakeVolumeMulti(divname, voldiv->GetMedium());
   vmulti->AddVolume(vol);
   voldiv->SetFinder(finder);
   finder->SetDivIndex(voldiv->GetNdaughters());
   for (Int_t ic=0; ic<ndiv; ic++) {
      voldiv->AddNodeOffset(vol, ic, start+step/2.+ic*step, opt.Data());
      ((TGeoNodeOffset*)voldiv->GetNodes()->At(voldiv->GetNdaughters()-1))->SetFinder(finder);    
   }
   return vmulti;
}   

//_____________________________________________________________________________
 Double_t TGeoPara::GetAxisRange(Int_t iaxis, Double_t &xlo, Double_t &xhi) const
{
// Get range of shape for a given axis.
   xlo = 0;
   xhi = 0;
   Double_t dx = 0;
   switch (iaxis) {
      case 1:
         xlo = -fX;
         xhi = fX;
         dx = xhi-xlo;
         return dx;
      case 2:
         xlo = -fY;
         xhi = fY;
         dx = xhi-xlo;
         return dx;
      case 3:
         xlo = -fZ;
         xhi = fZ;
         dx = xhi-xlo;
         return dx;
   }
   return dx;
}         
            
//_____________________________________________________________________________
 void TGeoPara::GetBoundingCylinder(Double_t *param) const
{
//--- Fill vector param[4] with the bounding cylinder parameters. The order
// is the following : Rmin, Rmax, Phi1, Phi2
   TGeoBBox::GetBoundingCylinder(param);
}   

//_____________________________________________________________________________
 Int_t TGeoPara::GetFittingBox(const TGeoBBox *parambox, TGeoMatrix *mat, Double_t &dx, Double_t &dy, Double_t &dz) const
{
// Fills real parameters of a positioned box inside this. Returns 0 if successfull.
   dx=dy=dz=0;
   if (mat->IsRotation()) {
      Error("GetFittingBox", "cannot handle parametrized rotated volumes");
      return 1; // ### rotation not accepted ###
   }
   //--> translate the origin of the parametrized box to the frame of this box.
   Double_t origin[3];
   mat->LocalToMaster(parambox->GetOrigin(), origin);
   if (!Contains(origin)) {
      Error("GetFittingBox", "wrong matrix - parametrized box is outside this");
      return 1; // ### wrong matrix ###
   }
   //--> now we have to get the valid range for all parametrized axis
   Double_t dd[3];
   dd[0] = parambox->GetDX();
   dd[1] = parambox->GetDY();
   dd[2] = parambox->GetDZ();
   //-> check if Z range is fixed
   if (dd[2]<0) {
      dd[2] = TMath::Min(origin[2]+fZ, fZ-origin[2]); 
      if (dd[2]<0) {
         Error("GetFittingBox", "wrong matrix");
         return 1;
      }
   }
   if (dd[0]>=0 && dd[1]>=0) {
      dx = dd[0];
      dy = dd[1];
      dz = dd[2];
      return 0;
   }
   //-> check now range at Z = origin[2] +/- dd[2]
   Double_t upper[8];
   Double_t lower[8];
   Double_t z=origin[2]-dd[2];
   lower[0]=z*fTxz-fTxy*fY-fX; 
   lower[1]=-fY+z*fTyz;
   lower[2]=z*fTxz+fTxy*fY-fX; 
   lower[3]=fY+z*fTyz;
   lower[4]=z*fTxz+fTxy*fY+fX; 
   lower[5]=fY+z*fTyz;
   lower[6]=z*fTxz-fTxy*fY+fX; 
   lower[7]=-fY+z*fTyz;
   z=origin[2]+dd[2];
   upper[0]=z*fTxz-fTxy*fY-fX; 
   upper[1]=-fY+z*fTyz;
   upper[2]=z*fTxz+fTxy*fY-fX; 
   upper[3]=fY+z*fTyz;
   upper[4]=z*fTxz+fTxy*fY+fX; 
   upper[5]=fY+z*fTyz;
   upper[6]=z*fTxz-fTxy*fY+fX; 
   upper[7]=-fY+z*fTyz;
   
   Double_t ddmin=TGeoShape::Big();
   for (Int_t iaxis=0; iaxis<2; iaxis++) {
      if (dd[iaxis]>=0) continue;
      ddmin=TGeoShape::Big();
      for (Int_t ivert=0; ivert<4; ivert++) {
         ddmin = TMath::Min(ddmin, TMath::Abs(origin[iaxis]-lower[2*ivert+iaxis]));
         ddmin = TMath::Min(ddmin, TMath::Abs(origin[iaxis]-upper[2*ivert+iaxis]));
      }
      dd[iaxis] = ddmin;
   }
   dx = dd[0];
   dy = dd[1];
   dz = dd[2];
   return 0;
}   

//_____________________________________________________________________________
 TGeoShape *TGeoPara::GetMakeRuntimeShape(TGeoShape *mother, TGeoMatrix * /*mat*/) const
{
// in case shape has some negative parameters, these has to be computed
// in order to fit the mother
   if (!TestShapeBit(kGeoRunTimeShape)) return 0;
   if (!mother->TestShapeBit(kGeoPara)) {
      Error("GetMakeRuntimeShape", "invalid mother");
      return 0;
   }
   Double_t dx, dy, dz;
   if (fX<0) dx=((TGeoPara*)mother)->GetX();
   else dx=fX;
   if (fY<0) dy=((TGeoPara*)mother)->GetY();
   else dy=fY;
   if (fZ<0) dz=((TGeoPara*)mother)->GetZ();
   else dz=fZ;
   return (new TGeoPara(dx, dy, dz, fAlpha, fTheta, fPhi));
}

//_____________________________________________________________________________
 void TGeoPara::InspectShape() const
{
// print shape parameters
   printf("*** Shape %s: TGeoPara ***\n", GetName());
   printf("    dX = %11.5f\n", fX);
   printf("    dY = %11.5f\n", fY);
   printf("    dZ = %11.5f\n", fZ);
   printf("    alpha = %11.5f\n", fAlpha);
   printf("    theta = %11.5f\n", fTheta);
   printf("    phi   = %11.5f\n", fPhi);
   printf(" Bounding box:\n");
   TGeoBBox::InspectShape();
}

//_____________________________________________________________________________
 Double_t TGeoPara::Safety(Double_t *point, Bool_t in) const
{
// computes the closest distance from given point to this shape, according
// to option. The matching point on the shape is stored in spoint.
   Double_t saf[3];
   // distance from point to higher Z face
   saf[0] = fZ-TMath::Abs(point[2]); // Z

   Double_t yt = point[1]-fTyz*point[2];      
   saf[1] = fY-TMath::Abs(yt);       // Y
   // cos of angle YZ
   Double_t cty = 1.0/TMath::Sqrt(1.0+fTyz*fTyz);

   Double_t xt = point[0]-fTxz*point[2]-fTxy*yt;      
   saf[2] = fX-TMath::Abs(xt);       // X
   // cos of angle XZ
   Double_t ctx = 1.0/TMath::Sqrt(1.0+fTxy*fTxy+fTxz*fTxz);
   saf[2] *= ctx;
   saf[1] *= cty;
   if (in) return saf[TMath::LocMin(3,saf)];
   for (Int_t i=0; i<3; i++) saf[i]=-saf[i];
   return saf[TMath::LocMax(3,saf)];
}

//_____________________________________________________________________________
 void TGeoPara::SavePrimitive(ofstream &out, Option_t * /*option*/)
{
// Save a primitive as a C++ statement(s) on output stream "out".
   if (TObject::TestBit(kGeoSavePrimitive)) return;
   out << "   // Shape: " << GetName() << " type: " << ClassName() << endl;
   out << "   dx    = " << fX << ";" << endl;
   out << "   dy    = " << fY << ";" << endl;
   out << "   dz    = " << fZ << ";" << endl;
   out << "   alpha = " << fAlpha<< ";" << endl;
   out << "   theta = " << fTheta << ";" << endl;
   out << "   phi   = " << fPhi << ";" << endl;
   out << "   TGeoShape *" << GetPointerName() << " = new TGeoPara(\"" << GetName() << "\",dx,dy,dz,alpha,theta,phi);" << endl;  
   TObject::SetBit(TGeoShape::kGeoSavePrimitive);
}

//_____________________________________________________________________________
 void TGeoPara::SetDimensions(Double_t *param)
{
// Set dimensions starting from an array.
   fX     = param[0];
   fY     = param[1];
   fZ     = param[2];
   fAlpha = param[3];
   fTheta = param[4];
   fPhi   = param[5];
   fTxy = TMath::Tan(param[3]*TMath::DegToRad());
   Double_t tth = TMath::Tan(param[4]*TMath::DegToRad());
   Double_t ph  = param[5]*TMath::DegToRad();
   fTxz   = tth*TMath::Cos(ph);
   fTyz   = tth*TMath::Sin(ph);
}   

//_____________________________________________________________________________
 void TGeoPara::SetPoints(Double_t *points) const
{
// Create PARA mesh points
   if (!points) return;
   Double_t txy = fTxy;
   Double_t txz = fTxz;
   Double_t tyz = fTyz;
   *points++ = -fZ*txz-txy*fY-fX; *points++ = -fY-fZ*tyz; *points++ = -fZ;
   *points++ = -fZ*txz+txy*fY-fX; *points++ = +fY-fZ*tyz; *points++ = -fZ;
   *points++ = -fZ*txz+txy*fY+fX; *points++ = +fY-fZ*tyz; *points++ = -fZ;
   *points++ = -fZ*txz-txy*fY+fX; *points++ = -fY-fZ*tyz; *points++ = -fZ;
   *points++ = +fZ*txz-txy*fY-fX; *points++ = -fY+fZ*tyz; *points++ = +fZ;
   *points++ = +fZ*txz+txy*fY-fX; *points++ = +fY+fZ*tyz; *points++ = +fZ;
   *points++ = +fZ*txz+txy*fY+fX; *points++ = +fY+fZ*tyz; *points++ = +fZ;
   *points++ = +fZ*txz-txy*fY+fX; *points++ = -fY+fZ*tyz; *points++ = +fZ;
}

//_____________________________________________________________________________
 void TGeoPara::SetPoints(Float_t *points) const
{
// create sphere mesh points
   if (!points) return;
   Double_t txy = fTxy;
   Double_t txz = fTxz;
   Double_t tyz = fTyz;
   *points++ = -fZ*txz-txy*fY-fX; *points++ = -fY-fZ*tyz; *points++ = -fZ;
   *points++ = -fZ*txz+txy*fY-fX; *points++ = +fY-fZ*tyz; *points++ = -fZ;
   *points++ = -fZ*txz+txy*fY+fX; *points++ = +fY-fZ*tyz; *points++ = -fZ;
   *points++ = -fZ*txz-txy*fY+fX; *points++ = -fY-fZ*tyz; *points++ = -fZ;
   *points++ = +fZ*txz-txy*fY-fX; *points++ = -fY+fZ*tyz; *points++ = +fZ;
   *points++ = +fZ*txz+txy*fY-fX; *points++ = +fY+fZ*tyz; *points++ = +fZ;
   *points++ = +fZ*txz+txy*fY+fX; *points++ = +fY+fZ*tyz; *points++ = +fZ;
   *points++ = +fZ*txz-txy*fY+fX; *points++ = -fY+fZ*tyz; *points++ = +fZ;
}

//_____________________________________________________________________________
 void TGeoPara::Sizeof3D() const
{
// fill size of this 3-D object
   TGeoBBox::Sizeof3D();
}